贵州省黔东南州榕江县朗洞中学2023-2024学年九年级下学...

更新时间：2024-03-24 浏览次数：28 类型：月考试卷

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2024九下·榕江月考) 在下列图案中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九下·榕江月考) 如图所示的图形中，绕某点旋转180°后，不能与原来图形重合的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·榕江月考) 如图所示，已知△OAB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是（）

A . 150° B . 120° C . 90° D . 60°

答案解析收藏纠错 + 选题
4. (2024九下·榕江月考) 在△ABC中，tan A= $\text{[math]}$ ， cos B= $\text{[math]}$ ，则∠C的度数是（）

A . 30° B . 45° C . 60° D . 90°

答案解析收藏纠错 + 选题
5. (2024九下·榕江月考) 如图所示，点P在第二象限，OP与x轴负半轴的夹角是α，且OP=5，cos α= $\text{[math]}$ ，则点P的坐标是（）

A . (3，4) B . (-3，4) C . (-4，3) D . (-3，5)

答案解析收藏纠错 + 选题
6. (2024九下·榕江月考) 正六边形ABCDEF内接于☉O，正六边形的周长是12，则☉O的半径是（）

A . $\text{[math]}$ B . 2 C . 2 $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·榕江月考) 如图所示，☉A过点O(0，0)，C( $\text{[math]}$ ， 0)，D(0，1)，点B是x轴下方☉A上一点，连接BO，BD，则∠OBD的度数是（）

A . 15° B . 30° C . 45° D . 60°

答案解析收藏纠错 + 选题
8. (2024九下·榕江月考) 如图所示，在Rt△ABC中，∠C=90°，D为BC边上一点，∠DAC=30°，BD=2，AB=2 $\text{[math]}$ ，则AC的长是（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·榕江月考) 如图所示，山顶一铁塔AB在阳光下的投影 CD的长为6 m，此时太阳光与地面的夹角∠ACD=60°，则铁塔AB的高为（）

A . 3 m B . 6 $\text{[math]}$ m C . 3 $\text{[math]}$ m D . 2 $\text{[math]}$ m

答案解析收藏纠错 + 选题
10. (2024九下·榕江月考) 如图所示，在平面直角坐标系中，点A，B分别在x轴负半轴和y轴正半轴上，点C在OB上，OC∶BC=1∶2，连接AC，过点O作OP∥AB交AC的延长线于点P.若P(1，1)，则 tan∠OAP 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
11. (2024九下·榕江月考) 将一个棱长为3的正方体表面涂上颜色，再把它分割成棱长为1的小正方体，将它们全部放入一个不透明盒子中摇匀，随机取出一个小正方体，有三个面被涂色的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024九下·榕江月考) 小明随机地在如图所示的圆及其内部区域投针，则针扎到其内接等边三角形(阴影)区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ π C . $\text{[math]}$ D . $\text{[math]}$ π

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2024九下·榕江月考) 在Rt△ABC中，∠C=90°，AC=5，BC=12，则sinA=

答案解析收藏纠错 + 选题
14. (2024九下·榕江月考) 在△ABC中，若|2sin A- $\text{[math]}$ |与( $\text{[math]}$ -2cos B)²互为相反数，则∠C=.

答案解析收藏纠错 + 选题
15. (2024九下·榕江月考) 如图所示，已知△ABC的外接圆☉O的半径为3，AC=4，则sin B=.

答案解析收藏纠错 + 选题
16. (2024九下·榕江月考) 如图所示，测量船以20 n mile/h的速度沿正东方向航行并对某海岛进行测量，测量船在A处测得海岛上观测点D位于北偏东15°方向上，观测点C位于北偏东45°方向上，航行半个小时到达B点，这时测得海岛上观测点C位于北偏西45°方向上，若CD与AB平行，则CD= n mile(计算结果不取近似值).

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文h字说明、证明过程或演算步骤.

17. (2024九下·榕江月考) 解下列一元二次方程：
1. （1） x²+x-1=0；
2. （2） x²+4x-1=0.
答案解析收藏纠错 + 选题
18. (2024九下·榕江月考)
1. （1）在△ABC中，∠C=90°，∠A=60°，BC=8，求AB和AC的长；
2. （2）在△ABC中，∠C=90°，a= $\text{[math]}$ ，b=3 $\text{[math]}$ ，解这个直角三角形.
答案解析收藏纠错 + 选题
19. (2024九下·榕江月考) 如图所示，把一张矩形卡片ABCD放在每格宽度为 12 mm 的横格纸中，恰好四个顶点都在横格线上，已知∠α=36°，求矩形卡片的周长(精确到1 mm，参考数据：sin 36°≈0.6，cos 36°≈0.8，tan 36°≈0.7).

答案解析收藏纠错 + 选题
20. (2024九下·榕江月考) 如图所示，为测量一段笔直自西向东的河流的宽度，小明在南岸边B处测得对岸边A处一棵大树位于北偏东60°方向，他以1.5 m/s的速度沿着河岸向东步行40 s后到达C处，此时测得大树位于北偏东45°方向，试计算此段河面的宽度(结果取整数，参考数据： $\text{[math]}$ ≈1.732).

答案解析收藏纠错 + 选题
21. (2024九下·榕江月考) 如图所示，在△ABC中，∠B=45°，CD是AB边上的中线，过点D作DE⊥BC，垂足为E，若CD=5，sin∠BCD= $\text{[math]}$ .
1. （1）求BC的长；
2. （2）求∠ACB的正切值.
答案解析收藏纠错 + 选题
22. (2024九下·榕江月考) 为了测量高速公路某桥的桥墩高度，某数学兴趣小组在同一水平地面C、D两处实地测量，如图所示.在C处测得桥墩顶部A处的仰角为 $\text{[math]}$ 和桥墩底部B处的俯角为 $\text{[math]}$ ，在D处测得桥墩顶部A处的仰角为 $\text{[math]}$ ，测得C、D两点之间的距离为 $\text{[math]}$ ，直线 $\text{[math]}$ 、 $\text{[math]}$ 在同一平面内，请你用以上数据，计算桥墩 $\text{[math]}$ 的高度.（结果保留整数，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
23. (2024九下·榕江月考) 如图所示，AB是☉O的直径，点E是劣弧BD上一点，∠PAD=∠AED，且DE= $\text{[math]}$ ， AE平分∠BAD，AE与BD交于点F.
1. （1）求证：PA是☉O的切线；
2. （2）若tan∠DAE= $\text{[math]}$ ，求EF的长.
答案解析收藏纠错 + 选题
24. (2024九下·榕江月考) “五一”节期间，许多露营爱好者在郊区露营，为遮阳和防雨会搭建一种“天幕”(如图所示)，其截面示意图是轴对称图形，对称轴是垂直于地面的支杆AB，用绳子拉直AD后系在树干EF上的点E处，使得A，D，E在一条直线上，通过调节点E的高度可控制“天幕”的开合，AC=AD=2 m，BF=3 m.
1. （1）天晴时打开“天幕”，若∠α=65°，求遮阳宽度CD(结果精确到0.1 m)；
2. （2）下雨时收拢“天幕”，从65°减少到45°，求点E下降的高度(结果精确到0.1 m，参考数据：sin 65 °≈0.90，cos 65°≈0.42，tan 65°≈2.14， $\text{[math]}$ ≈1.41).
答案解析收藏纠错 + 选题
25. (2024九下·榕江月考) 阅读下列材料，并完成相应的任务.
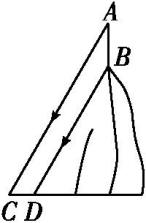
我们所学的锐角三角函数反映了直角三角形中的边角关系：
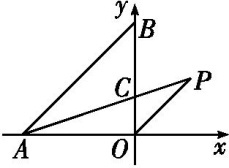
如图(1)所示.sin α= $\text{[math]}$ ， cos α= $\text{[math]}$ ，
tan α= $\text{[math]}$ .
一般地，当α，β为任意角时，sin(α+β)与sin(α-β)的值可以用下面的公式求得
sin(α+β)=sin αcos β+cos αsin β；sin(α-β)=sin α
cos β-cos αsin β.
例如：sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°
sin 30°= $\text{[math]}$ .
任务：
1. （1）计算：sin 75°=；
2. （2）如图(2)所示，在△ABC中，∠B=15°，∠C=45°，AC=2 $\text{[math]}$ -2，求AB和BC的长.
答案解析收藏纠错 + 选题