贵州省黔东南州从江县东朗中学2023-2024学年九年级上学...

更新时间：2024-03-22 浏览次数：16 类型：月考试卷

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2024九上·从江月考) 下列是冬季奥林匹克运动会会徽中的图案，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·从江月考) 若关于x的一元二次方程x²+(k+3)x+2=0的一个根是-2，则另一个根是（）

A . 2 B . 1 C . -1 D . 0

答案解析收藏纠错 + 选题
3. (2024九上·从江月考) 关于x的方程kx²+2x-1=0无实数根，则k的取值范围是（）

A . k≠0 B . k<-1 C . k≤-1 D . k=-1

答案解析收藏纠错 + 选题
4. (2024九上·从江月考) 已知二次函数y=-2x²+4x-3，如果y随x的增大而减小，那么x的取值范围是（）

A . x≥1 B . x≥0 C . x≥-1 D . x≥-2

答案解析收藏纠错 + 选题
5. (2024九上·从江月考) 已知点A(x-2，3)与点B(x+4，y-5)关于原点对称，则（）

A . x=-1，y=2 B . x=-1，y=8 C . x=-1，y=-2 D . x=1，y=8

答案解析收藏纠错 + 选题
6. (2024九上·从江月考) 在联合会上，有A，B，C三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放最适当的位置是在△ABC的（）

A . 三边中线的交点 B . 三条角平分线的交点 C . 三边中垂线的交点 D . 三边上高的交点

答案解析收藏纠错 + 选题
7. (2024九上·从江月考) 如图所示，将△ABC绕点A顺时针旋转60°得到△AED，若线段AB=3，则BE等于（）

A . 3 B . 4 C . 6 D . 9

答案解析收藏纠错 + 选题
8. (2024九上·从江月考) 如图所示，在△ABC中，∠C=90°，AB=10，若以点C为圆心，CB为半径的圆恰好经过AB的中点D，则AC的长为（）

A . 5 B . 5 $\text{[math]}$ C . 5 $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
9. (2024九上·从江月考) 已知一个扇形的半径为60 cm，圆心角为150°，若用它做成一个圆锥的侧面，则这个圆锥的底面半径为（）

A . 12.5 cm B . 25 cm C . 50 cm D . 75 cm

答案解析收藏纠错 + 选题
10. (2024九上·从江月考) 如图所示，在矩形ABCD中，AB=2 $\text{[math]}$ ， BC=4，以点A为圆心，AD长为半径画弧交BC于点E，连接AE，则阴影部分的面积为（）

A . 6 $\text{[math]}$ - $\text{[math]}$ B . 4 $\text{[math]}$ - $\text{[math]}$ C . 6 $\text{[math]}$ - $\text{[math]}$ D . 6 $\text{[math]}$ - $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024九上·从江月考) 已知二次函数y=ax²+bx+c的图象如图所示，则下列叙述正确的是（）

A . abc<0 B . -3a+c<0 C . b²-4ac≥0 D . 将该函数图象向左平移2个单位长度后所得抛物线的解析式为y=ax²+c

答案解析收藏纠错 + 选题
12. (2024九上·从江月考) 如图所示，王虎使一长为4 cm，宽为3 cm的长方形木板，在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）

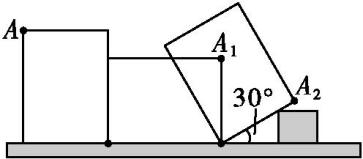
A . 10 cm B . 4π cm C . $\text{[math]}$ π cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2024九上·从江月考) 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 $\text{[math]}$ ，则n=．

答案解析收藏纠错 + 选题
14. (2024九上·从江月考) 如图所示，在一个长为 60 m，宽为40 m的矩形场地内修筑两条等宽的道路，剩余部分为绿化用地，如果绿化用地的面积为 2 204 m² ，那么道路的宽为 m.

答案解析收藏纠错 + 选题
15. (2024九上·从江月考) 二次函数y=ax²+bx+c的图象与x轴交于A，B两点，顶点为C，其中点A，C坐标如图所示，则一元二次方程ax²+bx+c=0的根是

答案解析收藏纠错 + 选题
16. (2024九上·从江月考) 如图所示，某大桥有一段抛物线形的拱梁，抛物线的解析式为y=ax²+bx.小强骑自行车从拱梁一端沿直线匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶10 s时和26 s时拱梁的高度相同，则小强骑自行车通过拱梁部分的桥面OC共需s.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2024九上·从江月考) 解方程：
1. （1） x²-4x-3=0；
2. （2） x²-4=3(x+2).
答案解析收藏纠错 + 选题
18. (2024九上·从江月考) 先化简，再求值.( $\text{[math]}$ -m+1)÷ $\text{[math]}$ ，其中m为一元二次方程x²+2x-5=0的根.

答案解析收藏纠错 + 选题
19. (2024九上·从江月考) 如图所示，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABO的三个顶点分别为 A(-1，3)，B(-4，3)，O(0，0).
1. （1）画出△ABO关于原点对称的图形△A₁B₁O，并写出点B₁的坐标；
2. （2）画出△ABO绕O点顺时针旋转90°后得到的图形△A₂B₂O，并写出点B₂的坐标.
答案解析收藏纠错 + 选题
20. (2024九下·凉州模拟) 小刚和小明两位同学玩一种游戏.游戏规则为：两人各执“象、虎、鼠”三张牌，同时各出一张牌定胜负，其中象胜虎、虎胜鼠、鼠胜象，若两人所出牌相同，则为平局.例如，小刚出象牌，小明出虎牌，则小刚胜；又如，两人同时出象牌，则两人平局.
1. （1）一次出牌小刚出“象”牌的概率是多少.
2. （2）如果用A，B，C分别表示小刚的象、虎、鼠三张牌，用A₁ ， B₁ ， C₁分别表示小明的象、虎、鼠三张牌，那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图法加以说明.
3. （3）你认为这个游戏对小刚和小明公平吗?为什么?
答案解析收藏纠错 + 选题
21. (2024九上·从江月考) 某水果店王阿姨到水果批发市场打算购进一种水果销售，经过讨价还价，实际价格每千克比原来少2元，发现原来买这种水果80千克的钱，现在可买 88千克.
1. （1）现在实际购进这种水果每千克多少元?
2. （2）王阿姨准备购进这种水果销售，若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.
  ①求y与x之间的函数解析式.
  ②请你帮王阿姨拿个主意，将这种水果的销售单价定为多少时，能获得最大利润?最大利润是多少?
答案解析收藏纠错 + 选题
22. (2024九上·从江月考) 如图所示，在△ABC中，AB=AC，AD⊥BC于点D，E是AB上一点，以CE为直径的☉O交BC于点F，连接DO，且∠DOC=90°.
1. （1）求证：AB是☉O的切线；
2. （2）若DF=2，DC=6，求BE的长.
答案解析收藏纠错 + 选题
23. (2024九上·从江月考) 如图所示，AB为☉O的直径，AC是☉O的一条弦，D为 $\text{[math]}$ 的中点，作DE⊥AC于点E，交AB的延长线于点F，连接DA.
1. （1）若AB=90 cm，则圆心O到EF的距离是多少?说明你的理由.
2. （2）若DA=DF=6 $\text{[math]}$ ，求阴影部分的面积(结果保留π).
答案解析收藏纠错 + 选题
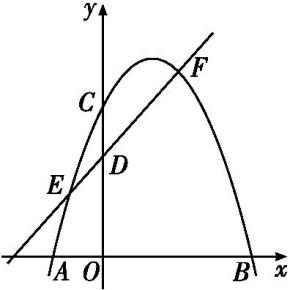
24. (2024九上·从江月考) 如图所示，在平面直角坐标系中，抛物线y=ax²+bx+3经过点 A(-1，0)，B(3，0)，与 y轴交于点C，直线 y=x+2与y轴交于点D，交抛物线于E，F两点，点P为线段EF上一个动点(与E，F不重合)，PQ∥y轴与抛物线交于点Q.
1. （1）求抛物线的解析式.
2. （2）当P在什么位置时，四边形PDCQ为平行四边形?求出此时点P的坐标.
答案解析收藏纠错 + 选题
25. (2024九上·从江月考) 【发现证明】如图(1)所示，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，在判断BE，EF，FD之间的数量关系时，小聪把△ABE绕点A逆时针旋转90°至△ADG，通过证明△AEF≌△AGF；从而发现并证明了EF=BE+FD.
1. （1）【类比引申】
  如图(2)所示，点E，F分别在正方形ABCD的边CB，CD的延长线上，∠EAF=45°，连接EF，请根据小聪的发现给你的启示写出EF，BE，DF之间的数量关系，并证明；
2. （2）【联想拓展】
  如图(3)所示，∠BAC=90°，AB=AC，点E，F在边BC上，且∠EAF=45°，若BE=3，EF=5，求CF的长.
答案解析收藏纠错 + 选题