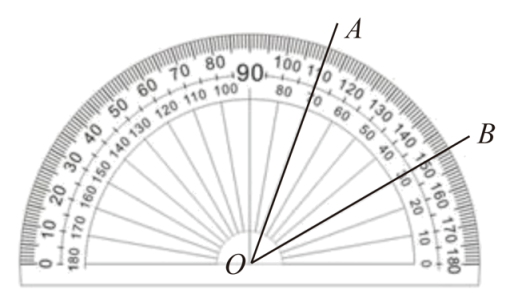

 B .
B .  D .
D . 

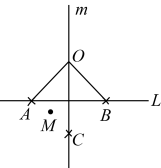
已知:是
的三个内角.
求证: .
有如下四个说法:①*表示内错角相等,两直线平行;②@表示;③上述证明得到的结论,只有在锐角三角形中才适用;④上述证明得到的结论,适用于任何三角形.其中正确的是( )
|
证明:如图,过点E作直线 使得 ∴
∴ |
方案Ⅰ:如图1,先过点B作 , 再在
上取C,D两点,使
, 接着过点D作
的垂线
, 交
的延长线于点E,则测量
的长即可;
方案Ⅱ:如图2,过点B作 , 再由点D观测,用测角仪在
的延长线上取一点C,使
, 则测量
的长即可.
对于方案Ⅰ、Ⅱ,说法正确的是( )

对于三人的答案,下列结论正确的是( )

验证:如,能被4整除,请把3与1的积写成两个正整数的平方差;
探究:设“发现”中两个正整数分别为m,n,请论证“发现”中的结论正确.
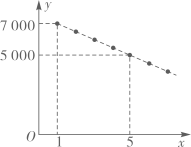
大棚面积 | 3 | 8 |
前期准备所需总费用/万元 | 21 | 134 |
