B . 
C . 
D . 
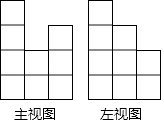
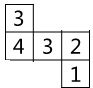
将相邻三个面的面积记为S1 ， S2 ， S3 ， 且S1<S2<S3的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体S1所在的面与x轴垂直，S2所在的面与y轴垂直，S3所在的面与z轴垂直，如图1所示。
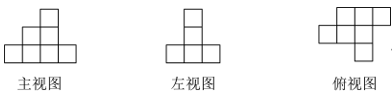
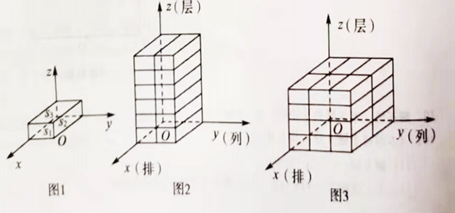
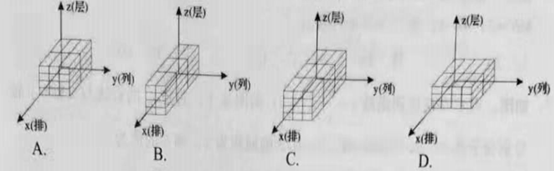
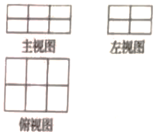
若将x轴方向表示的量称为几何体码放的排数，y轴方向表示的量称为几何体码放的列数，z轴方向表示的量称为几何体码放的层数；如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了1排2列6层，用有序数组记作(1，2，6)，如图3的几何体码放了2排3列4层，用有序数组记作(2，3，4)，这样我们就可用每一个有序数组(x，y，z)表示一种几何体的码放方式。
|
几何体有序数组 |
单位长方体的个数 |
表面上面积为S1的个数 |
表面上面积为S2的个数 |
表面上面积为S3的个数 |
表面积 |
|
（1，1，1） |
1 |
2 |
2 |
2 |
2S1+2S2+2S3 |
|
(1，2，1) |
2 |
4 |
2 |
4 |
4S1+2S2+4S3 |
|
(3，1，1) |
3 |
2 |
6 |
6 |
2S1+6S2+6S3 |
|
(2，1，2) |
4 |
4 |
8 |
4 |
4S1+8S2+4S3 |
|
(1，5，1) |
5 |
10 |
2 |
10 |
10S1+2S2+10S3 |
|
(1，2，3) |
6 |
12 |
6 |
4 |
12S1+6S2+4S3 |
|
(1，1，7) |
7 |
14 |
14 |
2 |
14S1+14S2+2S3 |
|
(2，2，2) |
8 |
8 |
8 |
8 |
8S1+8S2+8S3 |
|
…… |
…… |
…… |
…… |
…… |
…… |
根据以上规律，请直接写出有序数纰(x，y，z))的几何体表面积S(x，y，z)的计算公式；(用x，y，z，S1 ， S2 ， S3表示)
的图形，至少用多少个
？（ ）
， 从左面看到的形状图是
