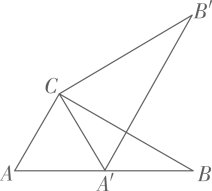
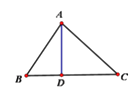
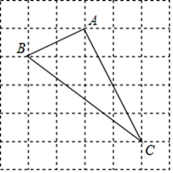
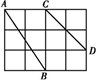
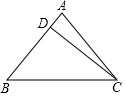
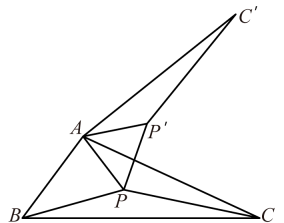
如图,点是
内的一点,将
绕点
逆时针旋转60°到
, 则可以构造出等边
, 得
,
, 所以
的值转化为
的值,当
,
,
,
四点共线时,线段
的长为所求的最小值,即点
为
的“费马点”.
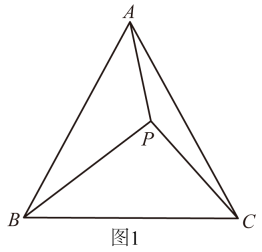
如图1,点是等边
内的一点,连接
,
,
, 将
绕点
逆时针旋转60°得到
.
①若 , 则点
与点
之间的距离是 ▲ ;
②当 ,
,
时,求
的大小;