浙江省杭州市萧山区城北片区2020-2021学年八年级上学期...

更新时间：2021-09-29 浏览次数：225 类型：期中考试

一、单选题

1. (2020八上·萧山期中) 下面的图形中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八上·萧山期中) 已知一个三角形的两条边长分别为4和6，则第三条边的长度不能是（）

A . 4 B . 7 C . 11 D . 3

答案解析收藏纠错 + 选题
3. (2024七下·麦积期中) 如果关于x的不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ，那么a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022八上·北仑期中) 一副三角板如图所示摆放，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020八上·萧山期中) 如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝10，EF＝2，那么AH等于（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
6. (2021八上·柯桥月考) 如图是用直尺和圆规作角平分线的示意图，通过证明△DOP≌△EOP可以说明OC是∠AOB的角平分线，那么△DOP≌△EOP的依据是（　　）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
7. (2020八上·萧山期中) 已知直角三角形纸片的两条直角边长分别为m和3（m $\text{[math]}$ 3），过锐角顶点把该纸片剪成两个三角形，若这两个三角形都为等腰三角形，则（）

A . m²+6m+9＝0 B . m²﹣6m+9＝0 C . m²+6m﹣9＝0 D . m²﹣6m﹣9＝0

答案解析收藏纠错 + 选题
8. (2020八上·颍州期末) 下列命题中，真命题有（）
①有一个角为60°的三角形是等边三角形；②底边相等的两个等腰三角形全等；③有一个角是40°，腰相等的两个等腰三角形全等；④一边上的中线等于这条边的一半的三角形是直角三角形.

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2020八上·萧山期中) 如图，在△ABC中，AC＝AB，∠BAC＝90°，BD平分∠ABC，与AC相交于点F，CD⊥BD，垂足为D，交BA的延长线于点E，AH⊥BC交BD于点M，交BC于点H，下列选项不正确的是（）

A . ∠E＝67.5° B . ∠AMF＝∠AFM C . BF＝2CD D . BD＝AB+AF

答案解析收藏纠错 + 选题
10. (2020八上·萧山期中) 如图，在锐角△ABC中，∠ACB＝50°；边AB上有一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最小时，∠MPN的度数是（）

A . 50° B . 60° C . 70° D . 80°

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·萧山期中) 已知命题“全等三角形的面积相等．”写出它的逆命题：，该逆命题是命题（填“真”或“假”)．

答案解析收藏纠错 + 选题
12. (2020八上·萧山期中) 疫情期间全国“停课不停学”初中生郑兴同学网上听课每节课a分钟，每天六节课，每天上网课总时长小于240分钟，可列不等式．

答案解析收藏纠错 + 选题
13. (2020八上·萧山期中) 等腰三角形的腰长为17，底长为16，则其底边上的高为.

答案解析收藏纠错 + 选题
14. (2020八上·萧山期中) 如图，在△ABC中，∠BAC＝90°，AB＝AC，点D，E均在边BC上，且∠DAE＝45°，若BD＝4，CE＝3，则DE＝.

答案解析收藏纠错 + 选题
15. (2020八上·萧山期中)
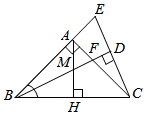
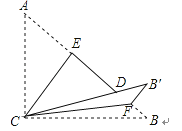
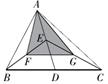
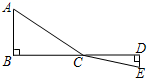
如图，Rt△ABC，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为

答案解析收藏纠错 + 选题
16. (2020八上·萧山期中) 如图，△ABC的面积是16，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是．

答案解析收藏纠错 + 选题

三、解答题

17. (2020八上·萧山期中)
1. （1）若x＞y，比较﹣3x+5与﹣3y+5的大小，并说明理由；
2. （2）若x＜y，且（a﹣3）x＞（a﹣3）y，求a的取值范围.
答案解析收藏纠错 + 选题
18. (2020八上·萧山期中) 如图
1. （1）如图（1），已知CE与AB交于点E，AC＝BC，∠1＝∠2．求证：△ACE≌△BCE．
2. （2）如图（2），已知CD的延长线与AB交于点E，AD＝BC，∠3＝∠4．探究AE与BE的数量关系，并说明理由．
答案解析收藏纠错 + 选题
19. (2020八上·萧山期中) 已知：如图，△ABC和△DCE都是等腰直角三角形，∠ACB＝∠DCE＝90°.
1. （1）求证：BD＝AE.
2. （2）若∠ABD＝∠DAE，AB＝8，AD＝6，求四边形ABED的面积.
答案解析收藏纠错 + 选题
20. (2020八上·萧山期中) 如图，已知等腰△ABC 中，AB=AC ， ∠A＜90°，CD 是△ABC 的高，BE 是△ABC 的角平分线，CD 与 BE 交于点 P ．当∠A 的大小变化时，△EPC 的形状也随之改变．
1. （1）当∠A=44°时，求∠BPD 的度数；
2. （2）设∠A=x°，∠EPC=y°，求变量 y 与 x 的关系式；
3. （3）当△EPC 是等腰三角形时，请直接写出∠A 的度数．
答案解析收藏纠错 + 选题
21. (2020八上·萧山期中) 如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，DE⊥BD，连结AC，CE.
1. （1）已知AB=3，DE=2，BD=12，设CD=x.用含x的代数式表示AC+CE的长；
2. （2）请问点C满足什么条件时，AC+CE的值最小？并求出它的最小值；
3. （3）根据（2）中的规律和结论，请构图求出代数式 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
22. (2020八上·萧山期中) 如图， $\text{[math]}$ 是边上的两点，点P从点A开始沿 $\text{[math]}$ 方向运动，且速度为每秒1cm，点Q从点B沿 $\text{[math]}$ 运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒.
1. （1）出发2秒后，求线段PQ的长；
2. （2）求点Q在BC上运动时，出发几秒后， $\text{[math]}$ 是等腰三角形；
3. （3）点Q在边CA上运动时，求能使 $\text{[math]}$ 成为等腰三角形的运动时间.
答案解析收藏纠错 + 选题
23. (2020八上·萧山期中) 在等腰三角形ABC中，
1. （1）若∠A＝110°，则∠B＝度；
2. （2）若∠A＝40°，则∠B＝ ▲ 度.
  通过上述解答，发现∠A的度数不同，得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中，设∠A＝α，求∠B的度数（用含α的式子表示）.请你根据∠B的度数的个数探索α的取值范围.
答案解析收藏纠错 + 选题