


 B .
B .  C .
C .  D .
D . 
![]()
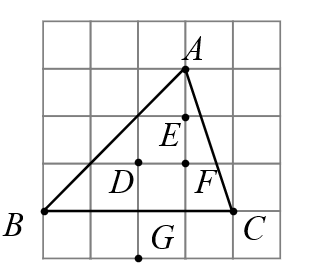
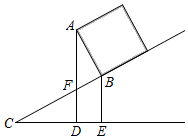
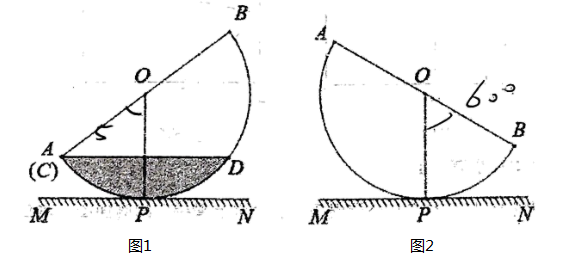
甲:如图1,当弦AB过点O时,EF与相切;
乙:如图2,当弦AB不过点O时,EF也与相切;
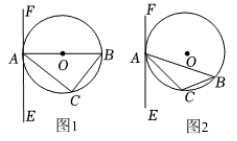
下列判断正确的是( )

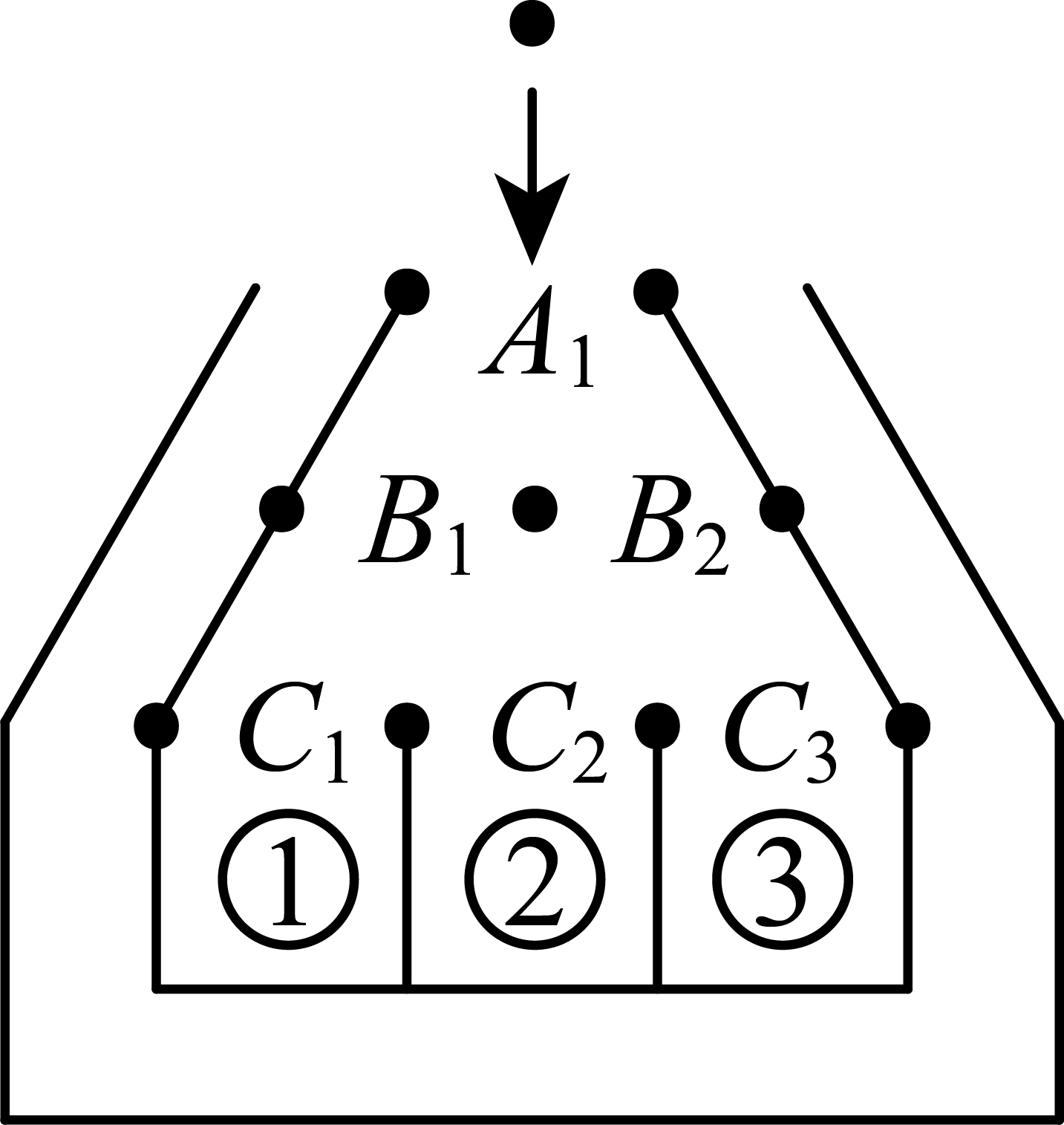
①当变化时,
随
的变化而变化,
与
满足函数关系
. ②无论n , r为何值,总有
. ③若
为定值,当
变化时,
随
的变化而变化,
与
满足二次函数关系.其中正确的是.(填序号).
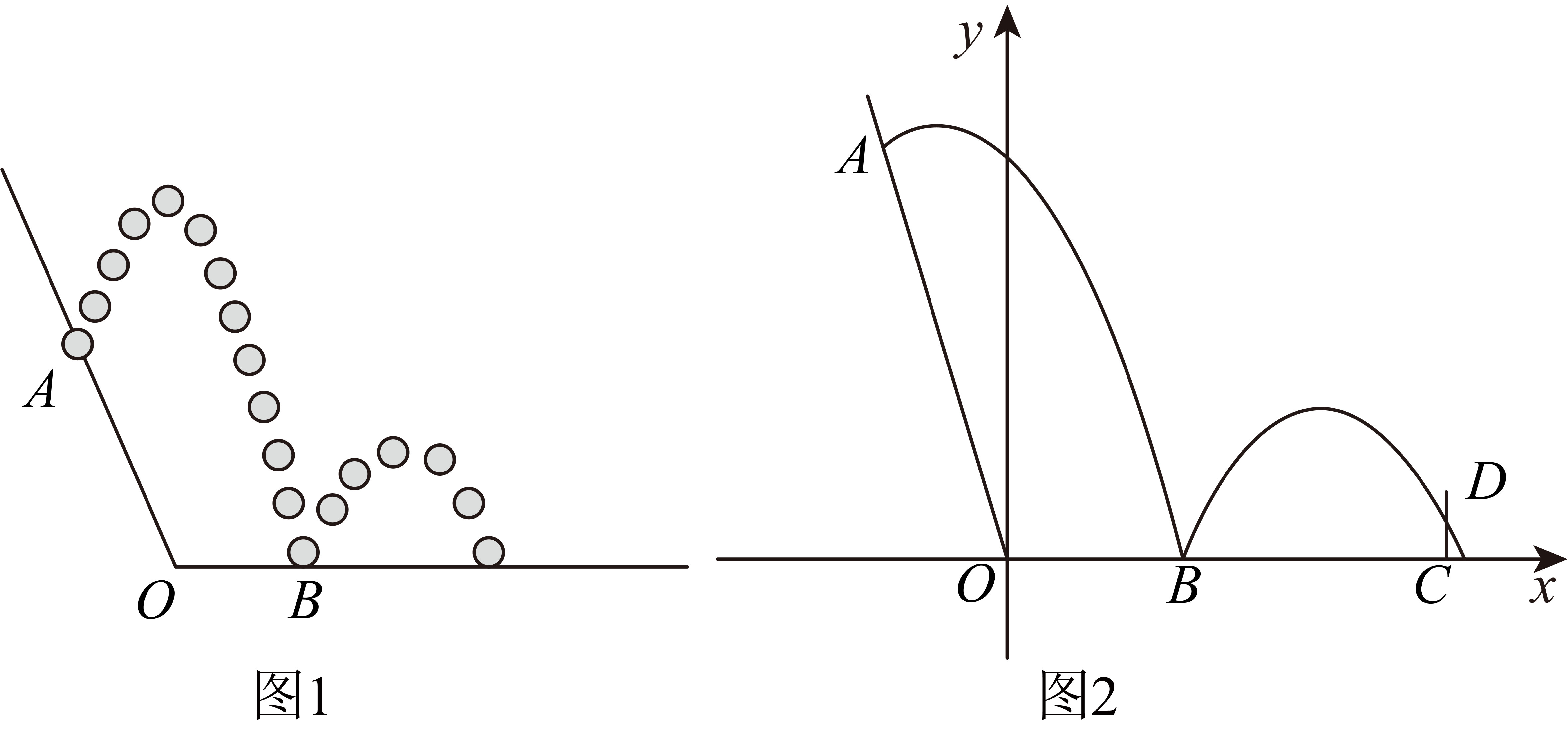

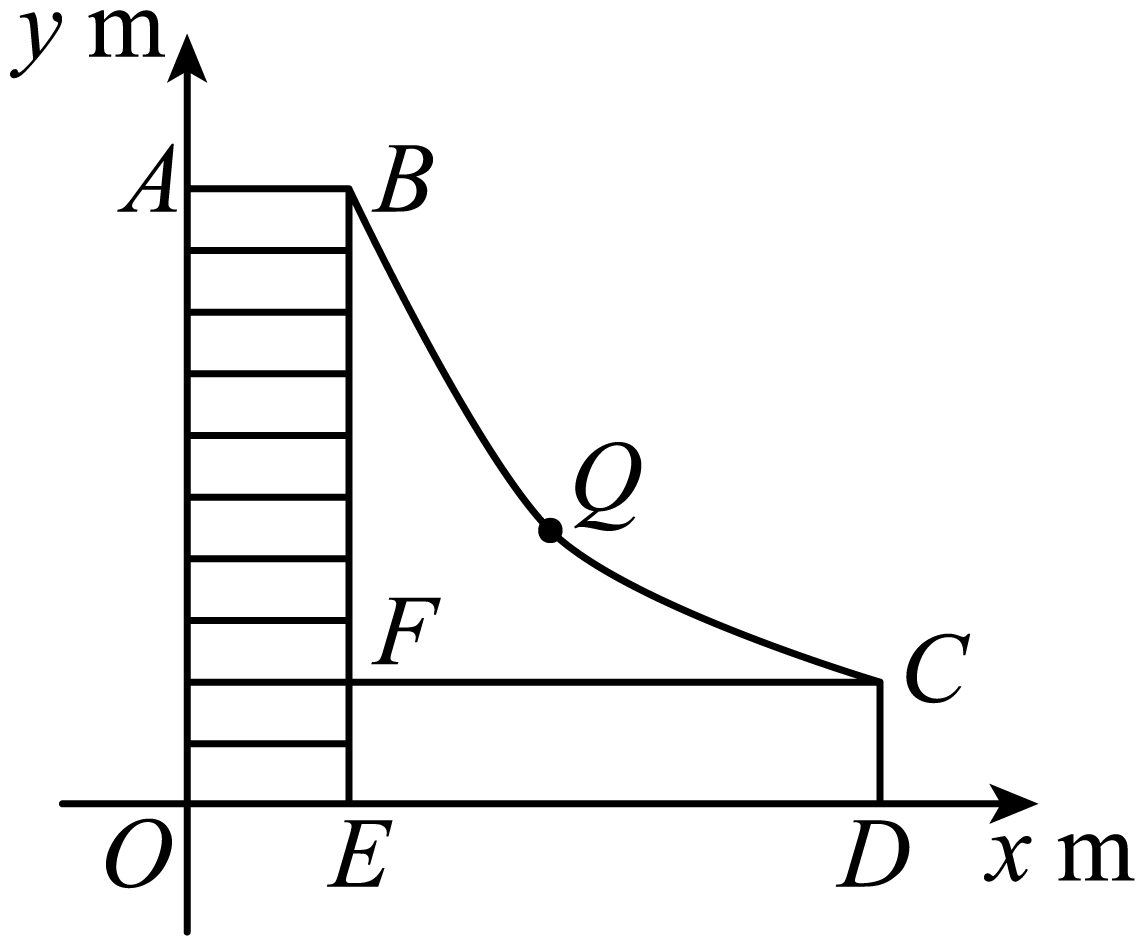
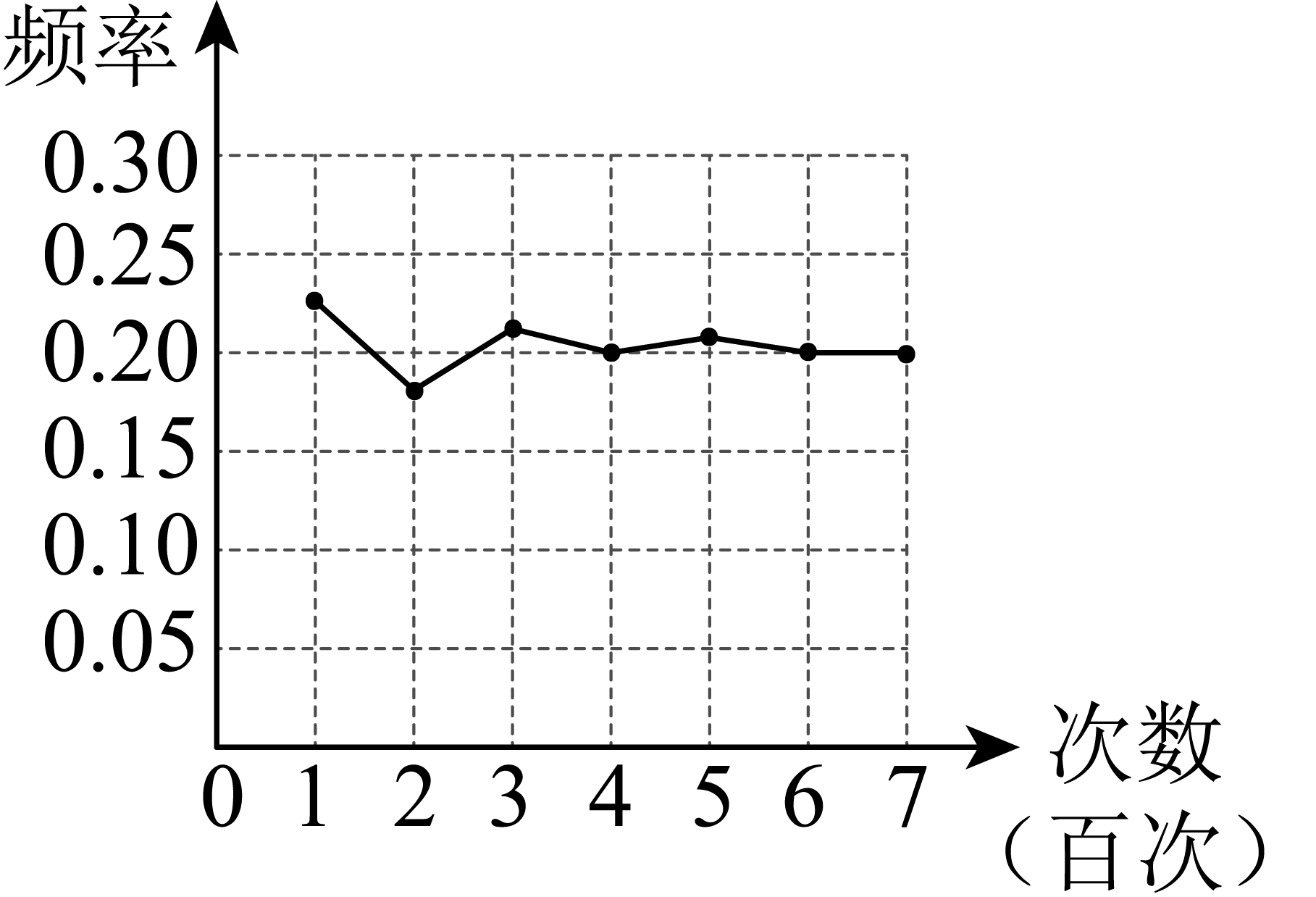
(参考数据: ,
,
)
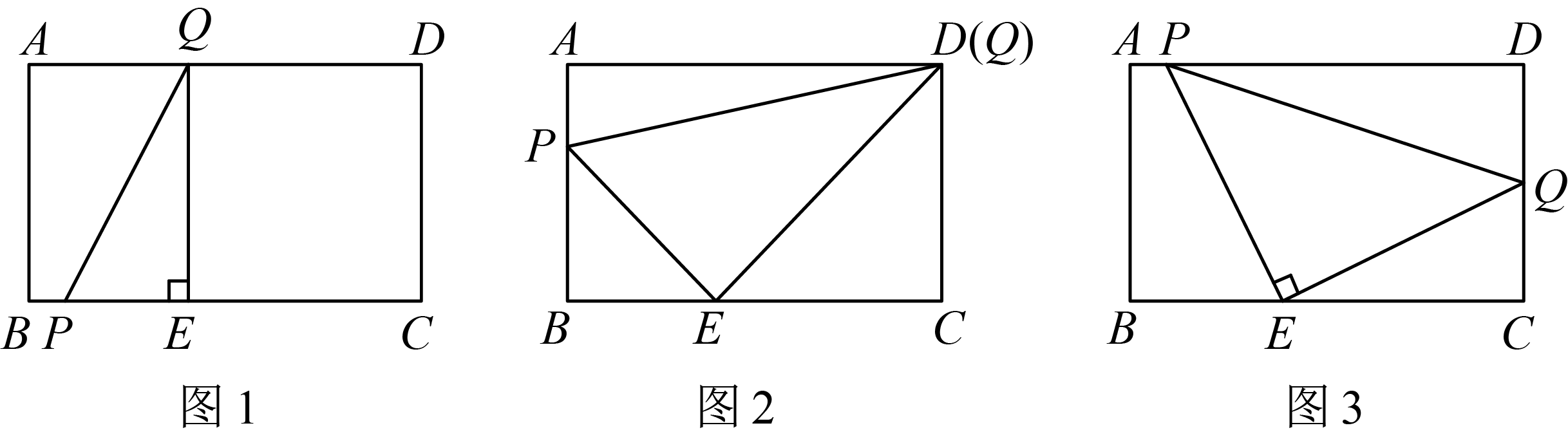
计算:在图1中.