广西壮族自治区南宁市部分学校2024年九年级一模考试数学模拟...

更新时间：2024-04-16 浏览次数：39 类型：中考模拟

一、选择题（共12小题，每小题3分，共36分，每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑.）

1. (2024九下·中山模拟) 2024年2月1日，某地记录到四个时刻的气温（单位：℃）分别为 $\text{[math]}$ ， 0，1， $\text{[math]}$ ，其中最低的气温是（）

A . $\text{[math]}$ B . 0 C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·南宁模拟) 如图所示的几何体是由6个完全相同的小正方体搭成，其主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024·南宁模拟) 截至2023年底，中国新能源汽车保有量已达 $\text{[math]}$ 辆，此数据用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·南宁模拟) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·南宁模拟) 在一个不透明的袋子里装有5个小球，这些小球除颜色外无其他差别，其中红球2个，白球3个，摇匀后，从这个袋子中任意摸出一个球，则这个球是白球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·会泽期中) 在平面直角坐标系中，点 $\text{[math]}$ 关于原点对称的点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·慈溪期中) 一元二次方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
8. (2024·南宁模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·南宁模拟) 某旅游景区内有一块三角形绿地 $\text{[math]}$ ，现要在绿地 $\text{[math]}$ 内建一个休息点 $\text{[math]}$ ，使它到 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三边的距离相等，下列作法正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2024·南宁模拟) 根据物理学知识，作用于物体上的压力 $\text{[math]}$ 所产生的压强 $\text{[math]}$ 与物体受力面积 $\text{[math]}$ 三者之间满足关系式 $\text{[math]}$ ，如果压力为 $\text{[math]}$ ，压强要大于 $\text{[math]}$ ，则下列关于 $\text{[math]}$ 的说法正确的是（）

A . $\text{[math]}$ 小于 $\text{[math]}$ B . $\text{[math]}$ 大于 $\text{[math]}$ C . $\text{[math]}$ 小于 $\text{[math]}$ D . $\text{[math]}$ 大于 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024·南宁模拟) 如图，在□ $\text{[math]}$ 中 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交边 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 8 B . 10 C . 12 D . 16

答案解析收藏纠错 + 选题
12. (2024·南宁模拟) 我们知道 $\text{[math]}$ ，小明同学据此画出了函数 $\text{[math]}$ 的大致图象，你认为小明同学所作图象正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分.）

13. (2024九下·古浪模拟) $\text{[math]}$ 的相反数是．

答案解析收藏纠错 + 选题
14. (2024八下·桂平期末) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2024·南宁模拟) 李校医对九（1）班50名学生的血型作了统计，列出如下边的统计表，则九（1）班 $\text{[math]}$ 型血的人数是．
血型
$\text{[math]}$ 型
$\text{[math]}$ 型
$\text{[math]}$ 型
$\text{[math]}$ 型
频率
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

答案解析收藏纠错 + 选题
16. (2024·南宁模拟) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的解，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
17. (2024·南宁模拟) 如图，当一个摆钟的钟摆 $\text{[math]}$ 从最左侧处摆到最右侧 $\text{[math]}$ 处时，摆角 $\text{[math]}$ ，点 $\text{[math]}$ 是弧 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为cm．（结果用含 $\text{[math]}$ 的式子表示）

答案解析收藏纠错 + 选题
18. (2024·南宁模拟) 如图，将一个边长为4的菱形 $\text{[math]}$ 沿着直线 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 延长线上的点 $\text{[math]}$ 处，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤.）

19. (2024七下·青秀月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024·南宁模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024·南宁模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 的三个顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）在图中画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ；
2. （2）将 $\text{[math]}$ 先向左平移4个单位长度，再向上平移2个单位长度，画出平移后的 $\text{[math]}$ ；
3. （3）在 $\text{[math]}$ 中有一点 $\text{[math]}$ ，则经过以上两次变换后点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标为．
答案解析收藏纠错 + 选题

22. (2024·南宁模拟) 2023年12月14日，一股冷空气开始影响我市，我市连续7天的天气情况如下：

上述天气情况包括了每天的天气状况（如阴转小雨，小雨转多云等），气温（如“4／ $\text{[math]}$ ”指当天最低和最高气温分别是 $\text{[math]}$ 和 $\text{[math]}$ ），风向和风级．

（1）这7天最高气温的众数是 $\text{[math]}$ ，中位数是 $\text{[math]}$ ；
（2）计算这7天最低气温的平均数；

（3）阅读冷空气等级标准表：

序号	等级	冷空气来临的48小时内气温变化情况
①	弱冷空气	降温幅度小于6 $\text{[math]}$
②	中等强度冷空气	降温幅度大于或等于6 $\text{[math]}$ ，但小于8 $\text{[math]}$
③	较强冷空气	降温幅度大于或等于8 $\text{[math]}$ ，且日最低气温超过8 $\text{[math]}$
④	强冷空气	降温幅度大于或等于8 $\text{[math]}$ ，且日最低气温不超过8 $\text{[math]}$
⑤	寒潮	降温幅度大于或等于10 $\text{[math]}$ ，且日最低气温不超过4 $\text{[math]}$

本次来临的冷空气的等级是．（填序号）

答案解析收藏纠错 + 选题

23. (2024·南宁模拟) 我国第一届全国学生（青年）运动会于2023年11月5日在广西南宁开幕，吉祥物“壮壮”和“美美”毛绒玩具在市场出现热销，已知“壮壮”比“美美”每个便宜40元，某商场用6400元购买“壮壮”的数量是用4800元购买“美美”数量的2倍．
1. （1）求购买一个“美美”和一个“壮壮”各需多少元？
2. （2）为满足顾客需求，商场从厂家一次性购买“壮壮”和“美美”共100个，要求购买的总费用不超过11020元，求最多可以购买“美美”多少个？
答案解析收藏纠错 + 选题
24. (2024·南宁模拟) 如图，已知 $\text{[math]}$ ，以 $\text{[math]}$ 为直径作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，作 $\text{[math]}$ 的平分线，交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
25. (2024·南宁模拟) 综合与实践
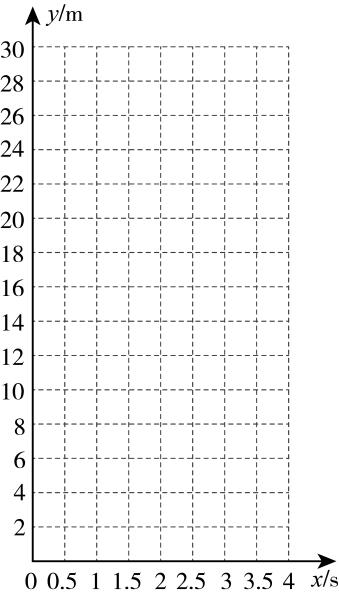
中国旅游研究院2024年1月5日发布的“2024年冰雪旅游十佳城市”中，哈尔滨位列榜首，火爆出圈，其中帽儿山的滑雪运动深受欢迎．滑雪爱好者小李为了得出滑行距离 $\text{[math]}$ （单位：m）与滑行时间 $\text{[math]}$ （单位：s）之间的关系，以便更好地享受此项运动所带来的乐趣，他在滑道A上设置了若干个观测点，收集一些数据，如下表所示：

点位1
点位2
点位3
点位4
点位5
点位6
点位7

滑行时间 $\text{[math]}$
0
0.5
1
1.5
2
2.5
3
…
滑行距离 $\text{[math]}$
0
1.625
4.5
8.625
14
20.625
28.5
1. （1）请你在平面直角坐标系中描出表中数据所对应的7个点，并用平滑的曲线连接它们；
2. （2）观察由（1）所得的图象，请你依图象选用一个函数近似地表示 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系，并求出这个近似函数的关系式（不要求写出自变量的取值范围）；
3. （3）若另一名滑雪爱好者小张在小李出发5秒后沿着滑道B滑行（两条滑道互相平行，且起点在同一直线上），他的滑行距离 $\text{[math]}$ （单位：m）与滑行时间 $\text{[math]}$ （单位：s）可近似地看成二次函数 $\text{[math]}$ ，当小李滑行距离为384m时，他比小张多滑行的距离不超过160m，求 $\text{[math]}$ 的最小值．（参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
26. (2024·南宁模拟) 应用与探究
【情境呈现】
在一次数学兴趣小组活动中，小明同学将一大一小两个三角板按照如图1所示的方式摆放，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．他把三角板 $\text{[math]}$ 固定好后，将三角板 $\text{[math]}$ 从图1所示的位置开始绕点 $\text{[math]}$ 按顺时针方向旋转，每秒转动 $\text{[math]}$ ，设转动时间为 $\text{[math]}$ 秒 $\text{[math]}$ ．
1. （1）【问题应用】请直接写出图1中线段 $\text{[math]}$ 的值；
2. （2）如图2，在三角板 $\text{[math]}$ 旋转的过程中，连接 $\text{[math]}$ ，当四边形 $\text{[math]}$ 是矩形时，求 $\text{[math]}$ 值；
3. （3）【问题探究】如图3，在三角板 $\text{[math]}$ 旋转的过程中，取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 是否存在最大值？若存在，请求出 $\text{[math]}$ 的最大值，并直接写出此时的 $\text{[math]}$ 值：若不存在，请说明理由．
答案解析收藏纠错 + 选题