广东省肇庆市高新区2023-2024学年九年级下册数学三月质...

更新时间：2024-08-28 浏览次数：8 类型：月考试卷

一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把正确的答案写在答题卡.

1. (2024九下·肇庆月考) 2024的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 024 D . 2024

答案解析收藏纠错 + 选题
2. (2024九下·肇庆月考) 在 $\text{[math]}$ ， 0这四个数中，最小的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
3. (2024九下·东莞模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·西山月考) 已知 $\text{[math]}$ ，下列不等式变形中正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·永定期中) 下列从左到右的变形，是因式分解的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·大武口月考) 下列根式中，属于最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·龙华模拟) 我国的北斗卫星导航系统中有一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024八下·蚌埠月考) 一元二次方程 $\text{[math]}$ 的两根分别是 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则b的值为（）

A . 2 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·肇庆月考) 我国古代数学名著《九章算术》中记载了一个问题，大意是：有几个人一起去买一件物品，每人出9元，多4元；每人出8元，少5元．问有多少人？该物品价值多少元？如果设有人，该物品值 $\text{[math]}$ 元，那么可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·肇庆月考) 如图，抛物线 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，且与轴交于点 $\text{[math]}$ ，其中 $\text{[math]}$ ，则在结论① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 中，正确的个数有（）．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本大题6小题，每小题3分，共18分）

11. (2024九下·肇庆月考) 分解因式：3x²﹣6xy=．

答案解析收藏纠错 + 选题
12. (2024九下·肇庆月考) 使函数 $\text{[math]}$ 有意义的的取值范围是．

答案解析收藏纠错 + 选题
13. (2024九下·肇庆月考) 已知点 $\text{[math]}$ 关于原点的对称点在第一象限，则a的取值范围是．

答案解析收藏纠错 + 选题
14. (2024七下·来宾月考) 若 $\text{[math]}$ 是方程 $\text{[math]}$ 的解，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024九下·肇庆月考) 分式方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
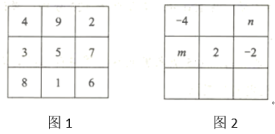
16. (2024九下·肇庆月考) 幻方的历史很悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方（如图1），将9个数填在3×3（三行三列）的方格中，如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等，就得到一个广义的三阶幻方．图2的方格中填写了一些数字和字母，若能构成一个广义的三阶幻方，则mn＝．

答案解析收藏纠错 + 选题

三、解答题（一）（17、18每题4分，19、20每题6分，共20分）

17. (2024九下·肇庆月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024九下·肇庆月考) 解不等式组 $\text{[math]}$ ，并把它的解集表示在数轴上．

答案解析收藏纠错 + 选题
19. (2024九下·肇庆月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024九下·肇庆月考) 一人一盔，安全守规，为保证市民安全出行，某商店以每顶50元的价格购进一批头盔，售价为每顶80元时，每月可售出200顶，在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶，若该商店每月获得的利润为8000元，求每顶头盔的售价是多少元？

答案解析收藏纠错 + 选题

四、解答题（二）（21题8分，22、23每题10分，共28分）

21. (2024九下·肇庆月考) 商店出售某品牌护眼灯，每台进价为40元，在销售过程中发现，月销量 $\text{[math]}$ （台）与销售单价（元）之间满足一次函数关系，规定销售单价不低于进价，且不高于进价的2倍，其部分对应数据如下表所示：
销售单价（元）
…
50
60
70
…
月销量 $\text{[math]}$ （台）
…
90
80
70
…
1. （1）求y与x之间的函数关系式；
2. （2）当护眼灯销售单价定为多少元时，商店每月出售这种护眼灯所获的利润最大？最大月利润为多少元？
答案解析收藏纠错 + 选题
22. (2024九下·肇庆月考) 《墨经》最早述及的小孔成像，是世界上最早的关于光学问题的论述，如图，根据小孔成像的科学原理，当像距（小孔到像的距离）和物高（蜡烛火焰高度）不变时，火焰的像高 $\text{[math]}$ （单位： $\text{[math]}$ ）是物距（小孔到蜡烛的距离）（单位： $\text{[math]}$ ）的反比例函数，当 $\text{[math]}$ 时， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 关于的函数解析式；
2. （2）若火焰的像高为 $\text{[math]}$ ，求小孔到蜡烛的距离．
答案解析收藏纠错 + 选题
23. (2024九下·肇庆月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿边 $\text{[math]}$ 向点B以 $\text{[math]}$ 的速度移动，点Q从B出发沿边BC向点 $\text{[math]}$ 以 $\text{[math]}$ 的速度移动， $\text{[math]}$ 两点同时出发，当一点到达终点时另一点也停止运动，设运动时间为 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 两点的距离为 $\text{[math]}$ 时，求的值？
2. （2）当为何值时，∆BPQ的面积最大？并求出最大面积．
答案解析收藏纠错 + 选题

五、解答题（三）（本大题2小题，每小题12分，共24分）

24. (2024九下·肇庆月考) 视力表中蕴含着很多数学知识，如：每个“E”形图都是正方形结构，同一行的“E”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表．
1. （1）素材1：国际通用的视力表以5米为检测距离，任选视力表中7个视力值n ，测得对应行的“E”形图边长b（mm），在平面直角坐标系中描点如图1．
  探究1：检测距离为5米时，归纳n与b的关系式，并求视力值1.2所对应行的“E”形图边长．
2. （2）素材2：图2为视网膜成像示意图，在检测视力时，眼睛能看清最小“E”形图所成的角叫做分辨视角，视力值与分辨视角（分）的对应关系近似满足 $\text{[math]}$ ．
  探究2：当 $\text{[math]}$ 时，属于正常视力，根据函数增减性写出对应的分辨视角的范围．
3. （3）素材3：如图3，当确定时，在A处用边长为 $\text{[math]}$ 的I号“E”测得的视力与在B处用边长为 $\text{[math]}$ 的Ⅱ号“E”测得的视力相同．
  探究3：若检测距离为3米，求视力值1.2所对应行的“E”形图边长．
答案解析收藏纠错 + 选题
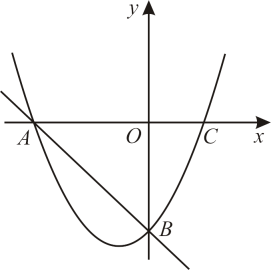
25. (2024九下·肇庆月考) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ （a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，－4），点C坐标为（2，0）.
1. （1）求此抛物线的函数解析式.
2. （2）点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由.
3. （3）点P为该抛物线对称轴上的动点，使得△PAB为直角三角形，请求出点P的坐标.
答案解析收藏纠错 + 选题