吉林省长春市榆树市部分学校2023-2024学年九年级下学期...

更新时间：2024-06-07 浏览次数：12 类型：开学考试

一、选择题（共8小题，每题3分，共24分）

1. (2017·泰兴模拟) 如图，是由几个小立方体所搭成的几何体的俯视图，小正方形中的数字表示在该位置上的立方体的个数，这个几何体的正视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九下·榆树月考) 下列二次根式中，是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·石景山期末) 若 $\text{[math]}$ ，则下列比例式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 如图，数轴上点A表示的数是2023，OA＝OB，则点B表示的数是（　　）

A . 2023 B . ﹣2023 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
5. 若关于x的一元二次方程2x²+x﹣m＝0有两个不相等的实数根，则m的取值范围是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·绿园期末) 如图，四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′＝2：3，四边形ABCD的面积等于4，则四边形A′B′C′D′的面积为（）

A . 3 B . 4 C . 6 D . 9

答案解析收藏纠错 + 选题
7. (2024九上·长春期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，利用尺规在 $\text{[math]}$ ， $\text{[math]}$ 上分别截取 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ；分别以 $\text{[math]}$ ， $\text{[math]}$ 为圆心、以大于 $\text{[math]}$ 的长为半径作弧，两弧在 $\text{[math]}$ 内交于点 $\text{[math]}$ ；作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上一动点，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·芝罘期中) 若抛物线y＝x²+bx+c的对称轴为y轴，且点P（2，6）在该抛物线上，则c的值为（　　）

A . ﹣2 B . 0 C . 2 D . 4

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

9. (2018·苏州) 若关于x的一元二次方程x²+mx+2n=0有一个根是2，则m+n=．

答案解析收藏纠错 + 选题
10. (2024九上·长春期末) 如图， $\text{[math]}$ 与 $\text{[math]}$ 位似，点 $\text{[math]}$ 为位似中心，若 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ，则 $\text{[math]}$ ： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. 已知二次函数y＝ax²+bx+c的函数值y与自变量x的部分对应值如表：
x
…
﹣2
﹣1
0
1
2
3
…
y
…
8
3
0
﹣1
0
3
…
则这个二次函数图象的对称轴是直线．

答案解析收藏纠错 + 选题
12. (2024九上·长春汽车经济技术开发期末) 如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在横格线上 $\text{[math]}$ 若线段 $\text{[math]}$ ，则线段 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. 如图，在平面直角坐标系中，P是第一象限的点，其坐标为（x ， 8），且OP与x轴正半轴的夹角α的正切值为 $\text{[math]}$ ，则x的值为．

答案解析收藏纠错 + 选题
14. 如图，△ABC与△DEF是位似图形，点O是位似中心，OB：BE＝1，若S_△_ABC＝2，则S_△_DEF＝．

答案解析收藏纠错 + 选题

三、解答题（共78分）

15. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024九下·榆树月考) 甲、乙两人同在如图所示的地下车库等电梯，已知他们分别在 $\text{[math]}$ 至 $\text{[math]}$ 层的任意一层出电梯．

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
车库
1. （1）如果甲在 $\text{[math]}$ 层出电梯，那么乙和甲在同一层楼出电梯的概率是；
2. （2）请你用画树状图 $\text{[math]}$ 或列表法 $\text{[math]}$ 求出甲、乙在同一楼层出电梯的概率．
答案解析收藏纠错 + 选题
17. 如图，公园原有一块长18m ，宽6m的矩形空地．后来从这块空地中划出不同区域种植不同品种的鲜花，中间铺设同样宽度的石子路将各区域间隔开．如果各区域鲜花面积和为85m² ，求所铺设的石子路的宽度．

答案解析收藏纠错 + 选题
18. 由小正方形构成的6×6网格中，每个正方形的顶点叫做格点．△ABC的顶点都在格点上，⊙O经过A、B、C三点，仅用无刻度的直尺在给定的网格中按要求作图（不写作法，保留作图痕迹）．
1. （1）图①中，画出⊙O的圆心O ．
2. （2）图②中，在BC边上找到一点D ，使得AD平分∠BAC；
3. （3）图③中，在⊙O上找到一点E（不与点C重合），使得 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2019·信丰模拟) 如图，一辆摩拜单车放在水平的地面上，车把头下方A处与坐垫下方B处在平行于地面的水平线上，A、B之间的距离约为49cm，现测得AC、BC与AB的夹角分别为45°与68°，若点C到地面的距离CD为28cm，坐垫中轴E处与点B的距离BE为4cm，求点E到地面的距离（结果保留一位小数）．（参考数据：sin68°≈0.93，cos68°≈0.37，cot68°≈0.40）

答案解析收藏纠错 + 选题
20. 在矩形ABCD中，E为DC边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F处．
1. （1）求证：△ABF∽△FCE；
2. （2）若AB＝8，AD＝10，求EC的长．
答案解析收藏纠错 + 选题
21. 【教材呈现】如图是华师版九年级上册数学教材第77页的部分内容．
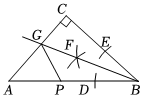
猜想：如图，在△ABC中，点D、E分别是AB与AC的中点．根据画出的图形，可以猜想：
DE∥BC ，且DE＝ $\text{[math]}$ BC
对此，我们可以用演绎推理给出证明．
1. （1）【定理证明】请根据教材内容，结合图①，写出证明过程．
2. （2）【定理应用】如图②，已知矩形ABCD中，AD＝6，CD＝4，点P在BC上从B向C移动，R、E、F分别是DC、AP、RP的中点，则EF＝．
3. （3）【拓展提升】如图③，△ABC中，AB＝12，BC＝16，点D ， E分别是AB ， AC的中点，点F在DE上，且∠AFB＝90°，则EF＝．
答案解析收藏纠错 + 选题
22. 某校为了解本校学生每天在校体育锻炼时间的情况，随机抽取了若干名学生进行调查，获得了他们每天在校体育锻炼时间的数据（单位：min），并对数据进行了整理、描述，部分信息如下：
a ．每天在校体育锻炼时间分布情况：
每天在校体育锻炼时间x（min）
频数（人）
百分比
60≤x＜70
14
14%
70≤x＜80
40
m
80≤x＜90
35
35%
x≥90
n
11%
b ．每天在校体育锻炼时间在80≤x＜90这一组的是：80，81，81，81，82，82，83，83，84，84，84，84，84，85，85，85，85，85，85，85，85，86，87，87，87，87，87，88，88，88，89，89，89，89，89．
根据以上信息，回答下列问题：
1. （1）表中m＝，n＝．
2. （2）若该校共有1000名学生，估计该校每天在校体育锻炼时间不低于80分钟的学生的人数；
3. （3）该校准备确定一个时间标准p（单位：min），对每天在校体育锻炼时间不低于p的学生进行表扬．若要使25%的学生得到表扬，则p的值可以是．
答案解析收藏纠错 + 选题
23. (2024九上·朝阳期末) 如图，一位足球运动员在距离球门中心水平距离8米的A处射门，球沿一条抛物线运动．当球运动的水平距离为6米时，达到最大高度3米．
1. （1）建立图中所示的平面直角坐标系，求抛物线所对应的函数表达式；
2. （2）已知球门高 $\text{[math]}$ 为2.44米，通过计算判断这位运动员能否将球射进球门．
答案解析收藏纠错 + 选题
24. (2020九上·二道期末) 如图，四边形ABCD是矩形，AB＝6，BC＝4，点E在边AB上（不与点A、B重合），过点D作DF⊥DE ，交边BC的延长线于点F ．
1. （1）求证：△DAE∽△DCF ．
2. （2）设线段AE的长为x ，线段BF的长为y ，求y与x之间的函数关系式．
3. （3）当四边形EBFD为轴对称图形时，则cos∠AED的值为．
答案解析收藏纠错 + 选题
25. 已知抛物线y＝ax²+bx+c（a、b、c是常数，a≠0），自变量x与函数值y的部分对应值如表：
x
0
1
2
3
…
y
﹣2
m
﹣2
1
…
1. （1）根据以上信息，可知抛物线开口向，对称轴为直线．
2. （2）求抛物线的解析式和m的值．
3. （3）将抛物线y＝ax²+bx+c（x＞0）的图象记为G₁ ，将G₁绕点O旋转180°后的图象记为G₂ ， G₁、G₂合起来得到的图象记为G ，完成以下问题：
  ①若直线y＝k与函数G有且只有两个交点，直接写出k的取值范围．
  ②若对于函数G上的两点P（x₁ ， y₁）、Q（x₂ ， y₂），当t≤x₁≤t+1，x₂≥2时，总有y₁＜y₂ ，直接写出t的取值范围．
答案解析收藏纠错 + 选题