四川省广安市岳池县2023-2024学年九年级下学期数学诊断...

更新时间：2024-05-16 浏览次数：25 类型：月考试卷

一、选择题(本大题共10个小题，每小题3分，共30分．每小题只有一个选项符合题意，请将所选选项填涂在答题卡相应位置上)

1. (2024九下·岳池月考) 实数2024的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -2024 D . 2024

答案解析收藏纠错 + 选题
2. (2024九下·岳池月考) 下列运算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·香坊模拟) 数据显示，截至2月17日16时，广安市28家开放的A级旅游景区在春节假期累计接待游客约160万人次．将160万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·岳池月考) 如图是某场比赛颁奖现场的领奖台的示意图，其主视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九下·岳池月考) 岳池顾县某豆干加工厂为调查一批豆干的品质，从中随机选取了6袋，记录其质量(单位：g)分别为 $\text{[math]}$ ，则这组数据的统计量中，是61的是（）

A . 只有众数、中位数 B . 只有众数、平均数 C . 只有中位数、平均数 D . 众数、中位数、平均数

答案解析收藏纠错 + 选题
6. (2024九下·岳池月考) 若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根，则下列 $\text{[math]}$ 的值中，不符合要求的是（）

A . 2 B . 1 C . 0 D . -1

答案解析收藏纠错 + 选题
7. (2024九下·岳池月考) 将直线 $\text{[math]}$ 向上平移3个单位长度，所得直线经过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . -11 B . -8 C . 7 D . 13

答案解析收藏纠错 + 选题
8. (2024九下·岳池月考) 在 $\text{[math]}$ 中，用直尺和圆规作图的痕迹如图所示．若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 10 B . 8 C . 6 D . 4

答案解析收藏纠错 + 选题
9. (2024九下·岳池月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以边 $\text{[math]}$ 为直径作 $\text{[math]}$ ，与线段 $\text{[math]}$ 的延长线分别交于点 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·岳池月考) 如图，二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，下列结论：(1) $\text{[math]}$ 0；(2) $\text{[math]}$ ；(3) $\text{[math]}$ ；(4)若 $\text{[math]}$ 两点在该二次函数的图象上，则 $\text{[math]}$ ．其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题(本大题共6个小题，每小题3分，共18分．请把最简答案填写在答题卡相应位置)

11. (2024八上·茂名月考) 9的算术平方根是．

答案解析收藏纠错 + 选题
12. (2024九下·岳池月考) 若在实数范围内 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是

答案解析收藏纠错 + 选题
13. (2024九下·岳池月考) 弹簧的长度 $\text{[math]}$ 与所挂物体的质量 $\text{[math]}$ 之间是一次函数关系，其图象如图所示，则弹簧未挂物体时的长度为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024九下·岳池月考) 若关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 无解，则 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
15. (2024九下·岳池月考) 如图， $\text{[math]}$ 是直线 $\text{[math]}$ 上长度固定为1的一条动线段．已知点 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为

答案解析收藏纠错 + 选题
16. (2024九下·岳池月考) 如图，在平面直角坐标系中，已知点 $\text{[math]}$ ，以 $\text{[math]}$ 为边在右侧作等边三角形 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ ，以 $\text{[math]}$ 为边在右侧作等边三角形 $\text{[math]}$ ，再过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ ，以 $\text{[math]}$ 为边在右侧作等边三角形 $\text{[math]}$ ，按此规律继续作下去，得到等边三角形 $\text{[math]}$ ，则点 $\text{[math]}$ 的纵坐标为

答案解析收藏纠错 + 选题

三、解答题(本大题共4个小题，第17小题5分，第18，19、20小题各6分，共23分

17. (2024九下·岳池月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024九下·岳池月考) 先化简： $\text{[math]}$ ，再从 $\text{[math]}$ 中选取合适的数作为 $\text{[math]}$ 的值，代入求值．

答案解析收藏纠错 + 选题
19. (2024九下·岳池月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 边的垂直平分线分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是菱形．

答案解析收藏纠错 + 选题
20. (2024九下·岳池月考) 如图，反比例函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象在第一象限交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ ，一次函数 $\text{[math]}$ 的图象分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）点 $\text{[math]}$ 的坐标为
2. （2）求一次函数的解析式及 $\text{[math]}$ 的值；
3. （3）直接写出当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题

四、实践应用题(本大题共4个小题，第21小题6分，第22、23、24小题各8分，共30分

21. (2024九下·岳池月考) 某校在课后延时服务中，成立了以下社团：A．计算机，B．围棋，C．篮球，D．书法，且每人只能加入一个社团．为了解学生参加社团的情况，从参加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图，其中图1中D对应扇形的圆心角为 $\text{[math]}$ ．
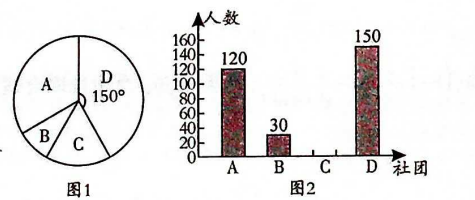
请结合图中所给信息，解答下列问题：
1. （1）这次被调查的学生共有人；若该校共有1500名学生加入了社团，则估计其中有名学生参加了计算机社团．
2. （2）请将条形统计图补充完整．
3. （3）在书法社团活动中，由于甲、乙、丙、丁四名同学平时的表现优秀，佮好其中有两名是男同学，两名是女同学．现决定从这四名同学中任选两名参加全市书法大赛，用画树状图或列表的方法，求恰好选中一男一女的概率．
答案解析收藏纠错 + 选题
22. (2024九下·岳池月考) 每年的4月23日为“世界读书日”．为了迎接第30个世界读书日，某校计划购进甲、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个、乙种书柜3个，共需资金1440元．
1. （1）甲、乙两种书柜每个的进价分别是多少元？
2. （2）若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多能够提供资金4320元，一共有哪几种购买方案？
答案解析收藏纠错 + 选题
23. (2024九下·岳池月考) 如图1，某款台灯由底座、支丵臂 $\text{[math]}$ 、连杆 $\text{[math]}$ 、悬臂 $\text{[math]}$ 和安装在 $\text{[math]}$ 处的光源组成．如图2是该款台灯放置在水平桌面上的侧面示意图，已知支撑臂 $\text{[math]}$ 桌面 $\text{[math]}$ ，固定 $\text{[math]}$ ，可通过调试悬臂 $\text{[math]}$ 与连杆 $\text{[math]}$ 的夹角提高照明效果．
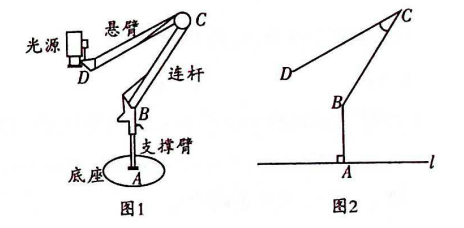
1. （1）悬臂端点 $\text{[math]}$ 到桌面 $\text{[math]}$ 的距离为多少厘米？
2. （2）已知当光源 $\text{[math]}$ 到桌面 $\text{[math]}$ 的距离为 $\text{[math]}$ 时照明效果较好，求此时悬臂 $\text{[math]}$ 与连杆 $\text{[math]}$ 的夹角 $\text{[math]}$ 的度数．
  (参考数据： $\text{[math]}$ )
答案解析收藏纠错 + 选题
24. (2024九下·岳池月考) 如图，网格中每个小正方形的边长为1．
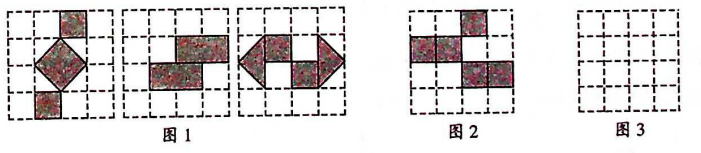
请你认真观察图1中的三个网格中的黑色部分构成的图案，解答下列问题：
1. （1）这三个图案都具有以下共同特征：都是对称图形，都不是对称图形；
2. （2）在图2中选一个白色的小正方形并涂黑，使图2中黑色部分是轴对称图形；
3. （3）请在图3中设计出一个面积为4的图案，且具备(1)中的特征(不与图1中所给图案相同)．
答案解析收藏纠错 + 选题

五、推理论证题(9分)

25. (2024九下·岳池月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线．
2. （2）若 $\text{[math]}$ ，求：
  ① $\text{[math]}$ 的值；
  ②线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

六、拓展探究题(10分)

26. (2024九下·岳池月考) 如图，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 两点，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）求抛物线的函数解析式．
2. （2）点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，与 $\text{[math]}$ 交于点 $\text{[math]}$ ，与抛物线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积的最大值．
3. （3）在抛物线的对称轴上是否存在点 $\text{[math]}$ ，使得以点 $\text{[math]}$ 为顶点的三角形是直角三角形？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题