湖南省岳阳市2024年中考第二次模拟考试数学试卷

更新时间：2024-12-24 浏览次数：9 类型：中考模拟

一、选择题（本大题共10小题，每小题3分，满分30分）

1. (2024九下·东港模拟) 在 $\text{[math]}$ 、 $\text{[math]}$ 、0、 $\text{[math]}$ 这四个数中，最大的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·岳阳模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·岳阳模拟) 下列图形中，是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024七下·沅江期末) 小明、小华、小亮、小雨4位同学在射箭训练中的平均成绩相同，他们的方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，你认为谁在训练中的发挥更稳定（）

A . 小明 B . 小华 C . 小亮 D . 小雨

答案解析收藏纠错 + 选题
5. (2024·岳阳模拟) 中央广播电视总台《2024年春节联欢晚会》以“龙行蠡蠡（da），欣欣家国”为主题，以“益”字为题眼，用“兢兢”之姿生动描摹1400000000中华儿女奋发有为、昂扬向上的精神风貌．其中数字1400000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·南宁期中) 已知点 $\text{[math]}$ ，均在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·海安期中) 若关于 $\text{[math]}$ 的二元一次方程组 $\text{[math]}$ 的解满足 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·长春月考) 2024年1月4日，第22届瓦萨国际滑雪节开幕式在长春净月潭国家森林公园启幕．如图，一名滑雪运动员沿着倾斜角为 $\text{[math]}$ 的斜坡，从点A滑行到点B ．若 $\text{[math]}$ ，则这名滑雪运动员水平方向BC滑行了多少米（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·岳阳模拟) 如图，在平行四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·岳阳模拟) 如图是二次函数 $\text{[math]}$ 的图象的一部分，给出下列命题：
① $\text{[math]}$ ；②方程 $\text{[math]}$ 的两根分别为 $\text{[math]}$ ， $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④ $\text{[math]}$ ；其中正确的命题是（）

A . ②③ B . ①② C . ①②③ D . ①②④

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，满分24分）

11. (2024·岳阳模拟) 要使根式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
12. (2024七下·武威期中) 若点P在y轴的左侧，到x轴的距离为3，到y轴的距离为2，则点P的坐标为．

答案解析收藏纠错 + 选题
13. (2024·岳阳模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024·岳阳模拟) 如图，在 $\text{[math]}$ 中，点M，N分别在边 $\text{[math]}$ 和 $\text{[math]}$ 上，且 $\text{[math]}$ ．若四边形 $\text{[math]}$ 的面积是 $\text{[math]}$ 面积的3倍，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024·岳阳模拟) 如图，已知 $\text{[math]}$ 的三个顶点都在 $\text{[math]}$ 上， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为°．

答案解析收藏纠错 + 选题
16. (2024·岳阳模拟) 从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，随机取一个数，取到无理数的概率为．

答案解析收藏纠错 + 选题
17. (2024九下·高密模拟) 对于实数x，用 $\text{[math]}$ 表示不超过x的最大整数，记 $\text{[math]}$ ．如 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则代数式 $\text{[math]}$ ．（要求答案为具体的数值）

答案解析收藏纠错 + 选题
18. (2024·岳阳模拟) 如图所示， $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，以 $\text{[math]}$ 为圆心的半圆分别与 $\text{[math]}$ 相切于 $\text{[math]}$ 两点，且 $\text{[math]}$ 的长度为 $\text{[math]}$ ，则图中的阴影部分面积为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，满分66分，解答应写出文字说明，证明过程或演算步骤）

19. (2024·岳阳模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2024·岳阳模拟) 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是平行四边形．

答案解析收藏纠错 + 选题
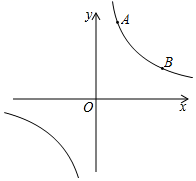
21. (2024·岳阳模拟) 反比例函数y= $\text{[math]}$ （k为常数，且k≠0）的图象经过点A（1，3）、B（3，m）.
1. （1）求反比例函数的解析式及B点的坐标；
2. （2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标.
答案解析收藏纠错 + 选题

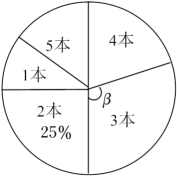
22. (2024·岳阳模拟) 4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然正气”．某校响应号召，开展了“读红色经典，传革命精神”为主题的读书活动，学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查，并对所有随机抽取的学生的读书量（单位：本）进行了统计．根据调查结果，绘制了不完整的统计表和扇形统计图．

读书量	1本	2本	3本	4本	5本
人数	10人	25人	30人	a	15人

（1）本次调查共抽取学生多少人？
（2）表中a的值为，扇形统计图中“3本”部分所对应的圆心角β的度数为．
（3）已知该校有3000名学生，请估计该校学生中，五月份读书量不少于“3本”的学生人数．

答案解析收藏纠错 + 选题

23. (2024九上·南昌月考) 建设美丽城市，改造老旧小区.某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同.
1. （1）求该市改造老旧小区投入资金的年平均增长率；
2. （2） 2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质，每个小区改造费用增加15%.如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？
答案解析收藏纠错 + 选题
24. (2024·岳阳模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，过圆上点 $\text{[math]}$ 的直线 $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2024·岳阳模拟)
1. （1）如图1，在 $\text{[math]}$ 中，D，E，F分别为 $\text{[math]}$ 上的点， $\text{[math]}$ 交 $\text{[math]}$ 于点G，求证： $\text{[math]}$ ．
2. （2）如图2，在（1）的条件下，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
3. （3）如图3，在 $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 交于点O，E为 $\text{[math]}$ 上一点， $\text{[math]}$ 交 $\text{[math]}$ 于点G， $\text{[math]}$ 交 $\text{[math]}$ 于点F．若 $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
26. (2024·岳阳模拟) 如图，抛物线 $\text{[math]}$ 与x轴相交于点A、点B，与y轴相交于点C．
1. （1）请直接写出点A，B，C的坐标；
2. （2）若点P是抛物线 $\text{[math]}$ 段上的一点，当 $\text{[math]}$ 的面积最大时求出点P的坐标，并求出 $\text{[math]}$ 面积的最大值；
3. （3）点F是抛物线上的动点，作 $\text{[math]}$ 交x轴于点E，是否存在点F，使得以A、C、E、F为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题