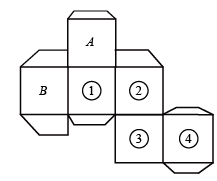
 B .
B .  C .
C .  D .
D . 







a . 甲滑雪场游客消费额的数据的频数分布直方图如下(数据分成6组: ,
,
,
,
,
):
b . 甲滑雪场游客消费额的数据在这一组的是:
410 430 430 440 440 440 450 450 520 540
c . 甲、乙两个滑雪场游客消费额的数据的平均数、中位数如表:
平均数 | 中位数 | |
甲滑雪场 | 420 | m |
乙滑雪场 | 390 | n |

根据以上信息,回答下列问题:

