题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广东省珠海市香洲区文园中学2023-2024学年七年级下学期...

更新时间：2024-05-09 浏览次数：39 类型：期中考试

一、选择题（本大题共10小题，每小题3分，共30分．在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．）

1. (2024七下·香洲期中) 数学课上老师用双手形象地表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）．从左至右依次表示（）

A . 同位角、内错角、同旁内角 B . 同旁内角、同位角、内错角 C . 同位角、对顶角、同旁内角 D . 同位角、内错角、对顶角

答案解析收藏纠错 + 选题
2. (2024七下·博罗期中) 下列各式中，是二元一次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·柳州期末) 下列四个数中，是无理数的是（）

A . 3.14 B . $\text{[math]}$ C . $\text{[math]}$ D . 0

答案解析收藏纠错 + 选题
4. (2024七下·香洲期中) 如图，下列条件不能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八上·桂林期末) 下列命题是真命题的是（）

A . 相等的角是对顶角 B . 两直线平行，同旁内角相等 C . 两点之间直线最短 D . 邻补角互补

答案解析收藏纠错 + 选题
6. (2024七下·香洲期中) 在下列各式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·香洲期中) 如图，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，使点A落在 $\text{[math]}$ 边上的点F处， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·香洲期中) 二元一次方程2x+y=7的正整数解有（）

A . 1组 B . 2组 C . 3组 D . 4组

答案解析收藏纠错 + 选题
9. (2024七下·香洲期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则x为（）

A . 214 B . $\text{[math]}$ C . 2140 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·香洲期中) 如图，已知 $\text{[math]}$ ，点C在EF上， $\text{[math]}$ ， BC平分∠DCF ，且AC⊥BC ．则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ．其中正确的个数有（）

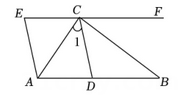
A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分．）

11. (2024七下·长沙期末) 已知 $\text{[math]}$ 是二元一次方程 $\text{[math]}$ 的一个解，则a的值为．

答案解析收藏纠错 + 选题
12. (2024七下·香洲期中) 若 $\text{[math]}$ 的平方根是 $\text{[math]}$ ，则a的值为．

答案解析收藏纠错 + 选题
13. (2024七下·香洲期中) 如图，已知直线AB ， CD相交于点O ， OE平分∠BOC ， $\text{[math]}$ ，则∠AOD的度数是°．

答案解析收藏纠错 + 选题
14. (2024七下·香洲期中) 已知关于x、y的方程组 $\text{[math]}$ ，则x+y的值为．

答案解析收藏纠错 + 选题
15. (2024七下·香洲期中) 一副三角板按图示摆放，点E恰好落在CB的延长线上，使 $\text{[math]}$ ，则∠BDE的大小为°．

答案解析收藏纠错 + 选题
16. (2024七下·香洲期中) 如图（一）所示的这种拼图（宽度设为acm）我们小时候可能都玩过，已知有若干片相同的拼图，且拼图依相同方向排列时可紧密拼成一行，如图（二）所示，当4片拼图紧密拼成一行时长度为19cm；如图（三）所示，当10片拼图紧密拼成一行时长度为46cm，则这样一片拼图的宽度a为cm．

答案解析收藏纠错 + 选题

三、解答题（一）（本大题共3小题，每小题7分，共21分．）

17. (2024七下·广州期末) 解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2024七下·香洲期中) 如图，已知 $\text{[math]}$ ，直线MN分别交AB ， CD于点E、F ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024七下·香洲期中) 如图，直线CD与直线AB相交于C ，请完成下列各题：
1. （1）过点P作 $\text{[math]}$ ，交AB于点Q；
2. （2）过点P作PR⊥CD ，垂足为R；
3. （3）连接PC ，比较线段PC与PR的长短，用“＜”连接，并说明依据．
答案解析收藏纠错 + 选题

四、解答题（二）（本大题共3小题，每小题9分，共27分．）

20. (2024七下·香洲期中) 某班为奖励在校运动会上取得好成绩的同学，花了200元购买甲、乙两种奖品共30件，其中甲种奖品每件8元，乙种奖品每件6元．求购买的甲、乙两种奖品各有多少件？

答案解析收藏纠错 + 选题
21. (2024七下·香洲期中) 如图，在△ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）判断EH和AD的位置关系，并说明理由；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求∠H的度数．
答案解析收藏纠错 + 选题
22. (2024七下·香洲期中) 如图两个4×4网格都是由16个边长为1的小正方形组成．
1. （1）图①中的阴影正方形的顶点在网格的格点上，这个阴影正方形的面积为，若这个正方形的边长为a ，则 $\text{[math]}$ ．
2. （2）观察图②，请先写出阴影部分的面积为，并在阴影部分的基础上将其补全为面积是5的正方形（顶点都在网格的格点上），若这个正方形的边长为b ，则 $\text{[math]}$ .
3. （3）请你利用以上结论，在图③的数轴上表示实数a和 $\text{[math]}$ 的大概位置．
答案解析收藏纠错 + 选题

五、解答题（三）（本大题共2小题，每小题12分，共24分．）

23. (2024七下·香洲期中) 已知△ABC中， $\text{[math]}$ ，将边AB沿着AC边所在直线平移得到线段DE（D与A为对应点且点D不与A、C重合），连接CE ．
1. （1）如图1，当BC⊥CE时，求∠E的度数；
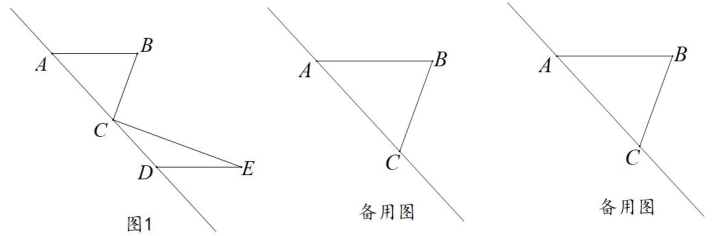
2. （2）在整个平移过程中，当 $\text{[math]}$ 时，求∠E的度数；
3. （3）在整个平移过程中，直接写出∠B、∠E、∠BCE之间的等量关系．
答案解析收藏纠错 + 选题
24. (2024七下·香洲期中) 任意一个无理数介于两个整数之间，我们定义，若无理数T： $\text{[math]}$ ，（其中m为满足不等式的最大整数，n为满足不等式的最小整数），则称无理数T的“麓外区间”为（m ， n），
如 $\text{[math]}$ ，所以 $\text{[math]}$ 的麓外区间为（1，2）．
1. （1）无理数 $\text{[math]}$ 的“麓外区间”是；
2. （2）实数x ， y ， m满足关系式：
  $\text{[math]}$
  求m的算术平方根的“麓外区间”．
3. （3）若某一个无理数T的“麓外区间”为（m ， n），其中 $\text{[math]}$ 是关于x ， y的二元一次方程 $\text{[math]}$ 的一组正整数解，请求出m、n的值，并写出一个符合题意的无理数T ．
答案解析收藏纠错 + 选题

试卷信息