题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川省自贡市蜀光绿盛实验学校2023-2024学年八年级下学...

更新时间：2024-06-18 浏览次数：20 类型：月考试卷

一、单项选择题（每题3分，共24分）

1. (2024八下·南昌期中) 下列式子中，是二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·自贡月考) 下列计算正确的是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·吉林期末) 下列各组数中，能构成直角三角形的是（　　）

A . 1，2，3 B . 5，7，10 C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D . 5，12，14

答案解析收藏纠错 + 选题
4. (2024八下·自贡月考) 下面四个二次根式中，最简二次根式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 $\text{[math]}$ D . $\text{[math]}$ （x≥0）

答案解析收藏纠错 + 选题
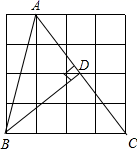
5. (2024八下·自贡月考) 如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
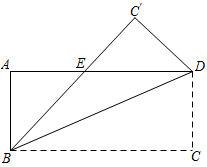
6. (2024八下·自贡月考) 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
7. (2024八下·自贡月考) 如图，将一根长25cm的细木棒放入长、宽、高分别为 $\text{[math]}$ 的长方体盒子中，则细木棒露在外面的最短长度是（）cm

A . 20 B . 15 C . 10 D . 5

答案解析收藏纠错 + 选题
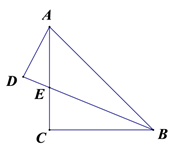
8. (2024八下·泗县期中) 如图，等腰直角△ABC中，AC=BC ， BE平分∠ABC ， AD⊥BE的延长线于点D ，若AD=2，则△ABE的面积为（）．

A . 4 B . 6 C . 2 $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

9. (2024八下·廉江期末) 若代数式 $\text{[math]}$ 有意义，则x的取值范围．

答案解析收藏纠错 + 选题
10. (2024八下·自贡月考) 如图，根据图中的标注和作图痕迹可知，在数轴上的点D所表示的数为．

答案解析收藏纠错 + 选题
11. (2024八下·乐陵月考) 若 $\text{[math]}$ 的整数部分是a，小数部分是b，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2024八下·自贡月考) 在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S₁ ， S₂ ， S₃ ， S₄ ，则S₁+S₂+S₃+S₄=．

答案解析收藏纠错 + 选题
13. (2024八下·自贡月考) 如图，长方体的上下底面是正方形，底面边长是 $\text{[math]}$ ，高为 $\text{[math]}$ ．在其侧面从点 $\text{[math]}$ 开始，绕侧面两周，嵌入装饰彩条至点 $\text{[math]}$ 停止，则彩条的最短长度为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024八下·自贡月考) 在 $\text{[math]}$ 中， $\text{[math]}$ 边上的高线为12，则 $\text{[math]}$ 的面积为.

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题5分，共25分）

15. (2024八下·自贡月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024八下·自贡月考) 先化简，再求值： $\text{[math]}$ ，其中a= $\text{[math]}$ +1．

答案解析收藏纠错 + 选题
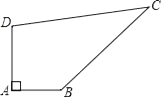
17. (2024八下·自贡月考) 已知某开发区有一块四边形的空地ABCD，如图所示，现计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，问要多少投入？

答案解析收藏纠错 + 选题
18. (2024八下·自贡月考) 已知实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值为多少？

答案解析收藏纠错 + 选题
19. (2024八下·自贡月考) 如图，有一艘货船和一艘客船同时从港口A出发，客船每小时比货船多走5海里，客船与货船速度之比为4：3，货船沿南偏东80°方向航行，2小时后，货船到达B处，客船到达C处，此时两船相距50海里．
1. （1）求两船速度分别是多少？
2. （2）求客船航行方向．
答案解析收藏纠错 + 选题

四、解答题（本大题共3个小题，每小题6分，共18分）

20. (2024八下·自贡月考) 已知x，y是实数，且满足y< $\text{[math]}$ ＋ $\text{[math]}$ ＋ $\text{[math]}$ ，化简： $\text{[math]}$ －(x－2＋ $\text{[math]}$ )².

答案解析收藏纠错 + 选题
21. (2024八下·大冶期中) 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
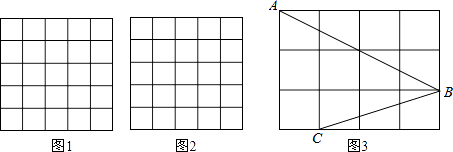
1. （1）在图1中以格点为顶点画一个面积为10的正方形；
2. （2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
答案解析收藏纠错 + 选题
22. (2024八下·自贡月考) 如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10点E是CD的中点，求AE的长．

答案解析收藏纠错 + 选题

五、解答题（本题共有2个小题，第23题7分，第24题8分，共15分）

23. (2024八下·自贡月考) 先阅读，再解答
由 $\text{[math]}$ =2可以看出，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式，在进行二次根式计算时，利用有理化因式，有时可以化去分母中的根号，例如： $\text{[math]}$ ，请完成下列问题：
1. （1） $\text{[math]}$ 的有理化因式是；
2. （2）化去式子分母中的根号： $\text{[math]}$ =， $\text{[math]}$ =；
3. （3）比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，并说明理由．
答案解析收藏纠错 + 选题
24. (2024八下·自贡月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若动点 $\text{[math]}$ 从点 $\text{[math]}$ 开始，按 $\text{[math]}$ 的路径运动，且速度为每秒 $\text{[math]}$ ，设出发的时间 $\text{[math]}$ 秒．
1. （1）出发2秒后，求 $\text{[math]}$ 周长；
2. （2）求当 $\text{[math]}$ 为何值时， $\text{[math]}$ 为等腰三角形．
3. （3）另有一点 $\text{[math]}$ ，从点 $\text{[math]}$ 开始，按 $\text{[math]}$ 的路径运动，且速度为每秒 $\text{[math]}$ ，若 $\text{[math]}$ 两点同时出发，当 $\text{[math]}$ 中有一点到达终点时，另一点也停止运动．当 $\text{[math]}$ 为何值时，直线 $\text{[math]}$ 把 $\text{[math]}$ 的周长分成相等的两部分？
答案解析收藏纠错 + 选题

试卷信息