湖北省黄石市大冶市2023-2024学年八年级下学期数学期中...

更新时间：2024-10-16 浏览次数：4 类型：期中考试

一、选择题（本大题共10个小题，每小题3分，共30分）

1. (2024九上·西城开学考) $\text{[math]}$ 在实数范围内有意义，则x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·雄安期末) 以下列各组数为边长，不能构成直角三角形的是（）

A . 3，4，5 B . 5，12，13 C . 6，7，8 D . 1， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·大冶期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·大冶期中) 下列命题中，假命题是（　　）

A . 对角线互相平分的四边形是平行四边形 B . 对角线互相平分且相等的四边形是矩形 C . 对角线互相垂直平分的四边形是菱形 D . 对角线互相垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
5. (2024八下·大冶期中) 下列各式中与 $\text{[math]}$ 是同类二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·大冶期中) 在如图所示的图形中，所有四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为5、6、20，则正方形B的面积是（）

A . 15 B . 9 C . 10 D . 21

答案解析收藏纠错 + 选题
7. (2024八下·大冶期中) 矩形具有而菱形不具有的性质是（　　）

A . 对角线相等 B . 对角线互相垂直 C . 对角线互相平分 D . 两组对角分别相等

答案解析收藏纠错 + 选题
8. (2024八下·大冶期中) 如图，菱形 $\text{[math]}$ 对角线 $\text{[math]}$ ， $\text{[math]}$ ，则菱形高 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024八下·大冶期中) 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， $\text{[math]}$ ，则下列结论：①∠CAD=30° ② $\text{[math]}$ ③S_{平行四边形}_ABCD=AB•AC ④ $\text{[math]}$ ，正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题（本大题共5个小题，每小题3分，共15分）

10. (2024八下·潮南期末) 若 $\text{[math]}$ 是整数，则正整数n的最小值为．

答案解析收藏纠错 + 选题
11. (2024八下·大冶期中) 化简： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024八下·大冶期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 是对角线，E ， F是对角线上的两点，要使四边形 $\text{[math]}$ 是平行四边形，还需添加一个条件（只需添加一个）是．

答案解析收藏纠错 + 选题
13. (2024八下·大冶期中) 如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标．

答案解析收藏纠错 + 选题
14. (2024八下·大冶期中) 如图，已知矩形ABCD ， $\text{[math]}$ ， $\text{[math]}$ ， E为CD边上一点， $\text{[math]}$ ，点P从B点出发，以每秒1个单位的速度沿着BA边向终点A运动，连接PE ，设点P运动的时间为t秒，则当t的值为时， $\text{[math]}$ 是以PE为腰的等腰三角形．

答案解析收藏纠错 + 选题

三、解答题（本大题共9个小题，共75分）

15. (2024八下·大冶期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. (2024八下·大冶期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）直接写出： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2024八下·大冶期中) 阅读与思考
请仔细阅读并完成相应任务：在解决问题“已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值”时，小明是这样分析与解答的：
∵ $\text{[math]}$
∴ $\text{[math]}$ ，∴ $\text{[math]}$ ，
∴ $\text{[math]}$ ．
任务：请你根据小明的分析过程，解决如下问题：若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
18. (2024八下·大冶期中) 消防车上的云梯示意图如图1所示，云梯最多只能伸长到15米，消防车高3米．如图2，某栋楼发生火灾，在这栋楼的B处有一老人需要救援，救人时消防车上的云梯伸长至最长，此时消防车的位置A与楼房的距离为12米．
1. （1）求B处与地面的距离．
2. （2）完成B处的救援后，消防员发现在B处的上方3米的D处有一小孩没有及时撤离，为了能成功地救出小孩，则消防车从A处向着火的楼房靠近的距离AC为多少米?
答案解析收藏纠错 + 选题
19. (2024八下·大冶期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点E ，延长BC至F点使 $\text{[math]}$ ，连接AF ， DE ， DF ．
1. （1）求证：四边形AEFD是矩形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求AE的长．
答案解析收藏纠错 + 选题
20. (2024八下·大冶期中) 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
1. （1）在图1中以格点为顶点画一个面积为10的正方形；
2. （2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
答案解析收藏纠错 + 选题
21. (2024八下·大冶期中) 如图，点D是线段AB的中点，点C是线段AB的垂直平分线上的任意点， $\text{[math]}$ 于点E ， $\text{[math]}$ 于点F ．
1. （1）判断 $\text{[math]}$ 的形状；
2. （2）求证： $\text{[math]}$ ；
3. （3）线段CD与AB满足什么数量关系时，四边形CEDF成为正方形？请说明理由．
答案解析收藏纠错 + 选题
22. (2024八下·大冶期中) 综合与实践：
综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
【操作判断】
1. （1）操作一：
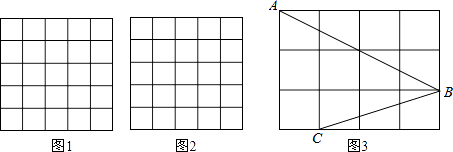
  如图1，正方形纸片 $\text{[math]}$ ，将 $\text{[math]}$ 沿过点A的直线折叠，使点B落在正方形 $\text{[math]}$ 的内部，得到折痕 $\text{[math]}$ ，点B的对应点为M ，连接 $\text{[math]}$ ；将 $\text{[math]}$ 沿过点A的直线折叠，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，得到折痕 $\text{[math]}$ ，将纸片展平，连接 $\text{[math]}$ ．
  根据以上操作，易得点E ， M ， F三点共线，且① $\text{[math]}$ °；②线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系为．
2. （2）【深入探究】
  操作二：
  如图2、将 $\text{[math]}$ 沿 $\text{[math]}$ 所在直线折叠，使点C落在正方形 $\text{[math]}$ 的内部，点C的对应点为N ，将纸片展平，连接 $\text{[math]}$ 、 $\text{[math]}$ ．
  同学们在折纸的过程中发现，当点E的位置不同时，点N的位置也不同，当点E在 $\text{[math]}$ 边上某一位置时（点E不与点B ， C重合），点N恰好落在折痕 $\text{[math]}$ 上，此时 $\text{[math]}$ 交 $\text{[math]}$ 于点P ，如图3所示．
  ①小明通过观察图形，测量并猜想，得到结论 $\text{[math]}$ ，请证明该结论是否成立，并说明理由．
  ②【拓展应用】若正方形纸片 $\text{[math]}$ 的边长为3，当点N落在折痕 $\text{[math]}$ 上时，求出线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2024八下·大冶期中) 如图，在直角坐标系中，点E为线段AB上一动点，点C为y轴上的一动点．
1. （1）如图（1），若 $\text{[math]}$ ，过点E作 $\text{[math]}$ 于点M ，连接CM ，设 $\text{[math]}$ ， $\text{[math]}$ ，判断四边形BCME的形状，请证明你的结论．
2. （2）如图（2），过点E作 $\text{[math]}$ 交OA于点D ，点F在线段AO上，设 $\text{[math]}$ ， $\text{[math]}$ ，且点 $\text{[math]}$ ．
  ①若四边形CEFD为平行四边形，用含t的式子表示点C的坐标．
  ②若四边形CEFD为菱形，求t的值．
答案解析收藏纠错 + 选题