①长方形的长和宽是两个变量；
②长方形的周长是自变量时，它的宽是因变量；
③长方形的长是自变量时，它的宽是因变量；
④长方形的宽是自变量时，它的长是因变量；
⑤长方形的长是自变量时，它的面积是因变量．
其中正确的说法有（ ）
B . 
C . 
D . 
①∠BOE＝70°②OF平分∠BOD ③∠POE＝∠BOF④∠POB＝2∠DOF
其中正确的结论的个数为（ ）
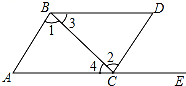
①甲车行驶的速度是60km/h，乙车行驶的速度是80km/h；
②甲出发4h后被乙追上；
③甲比乙晚到h；
④甲车行驶8h或h，甲，乙两车相距80km；
其中正确的是．
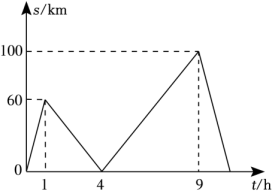
如图，已知点O ， E在直线AB上，OD是∠BOC的平分线，过点E作OD的平行线交OC于点F ， 试说明：∠1＝∠2．
说明：∵EF∥OD ，
∴∠3＝∠ ▲ （ ）．
∵EF∥OD ，
∴∠4＝∠ ▲ （ ）．
∵OD是∠BOC的平分线，
∴∠3＝∠4（ ）．
∴∠5＝∠6，
∵∠5+∠1＝180°，∠6+∠2＝180°，
∴∠1＝∠2（ ）．
自来水公司水费专用发票发票联
计费日期：2018.9.1﹣﹣2018.10.1
上期抄表数 | 本期抄表数 | 本期用水量 |
587 | 632 | 45 |
自来水费（含污水处理费） | ||
用水量（吨） | 单价（元/吨） | 金额（元） |
第一级：20 第二级：20 第三级：5 | 2.5 3.45 6.3 | 50 69 31.5 |
本期实付金额（大写）：壹佰伍拾元伍角整 小写金额：150.5元 | ||
备注：第一级为月用水量20吨及以下（含20吨）； 第二级为月用水量超过20吨，不超过40吨； 第三级为月用水量40吨以上（不含40吨）． | ||
我们在学习代数式求值时，遇到这样一类题：代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值．
通常的解题思路是：把x、y看作字母，a看作系数，合并同类项．因为代数式的值与x的取值无关，所以含x项的系数为0．
具体解题过程是：原式＝（a+3）x﹣6y+5，
∵代数式的值与x的取值无关，
∴a+3＝0，解得a＝﹣3．
若关于x的多项式m（2x﹣3）+2m2﹣4x的值与x的取值无关，求m值；
7张如图1的小长方形，长为a ， 宽为b ， 按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分都是长方形．设右上角的面积为S1 ， 左下角的面积为S2 ， 当AB的长变化时，S1﹣S2的值始终保持不变，求a与b的等量关系．
（1）如图1，当点B在直线MN上，点C在直线MN上方时，延长CB交直线PQ于点D ， 则∠CAB和∠CDP之间的数量关系是____．
