 B .
B .  C .
C .  D .
D . 
 B .
B . 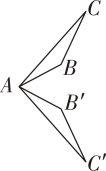 C .
C . 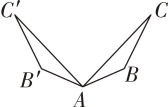 D .
D . 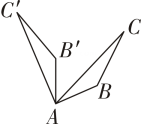

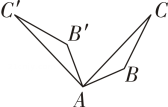
若将灯光装置改放在如图所示的点
,
或
处,能使表演区完全照亮的方案可能是( )
在
处放置
台该型号的灯光装置
在
,
处各放置
台该型号的灯光装置
在
处放置
台该型号的灯光装置
已知:直线和直线
外一点
.
求作:直线 , 使得
.
作法:如图,
在直线
上任取两点
,
;
以点
为圆心,
长为半径画弧,以点
为圆心,两弧在直线
上方交于点
:
作直线
.
直线就是所求作的直线.
根据小东设计的尺规作图过程,
证明:
,
,
四边形
是平行四边形
填写推理的依据
.
填写推理的依据
.
即 .
我们也可以逆用“三线合一”定理,证明这个三角形是等腰三角形,即:在三角形中,则这个三角形是等腰三角形结论
.
选择下面一种情况,完成证明.
情况一 | 情况二 | 情况三 |
已知:如图,在 | 已知:如图,在 | 已知:如图,在 |
选择情况: .
证明:


具体研究过程如下,请补充完整:
建立模型:设该容器的表面积为 , 底面半径为
, 高为
, 则
,
,
由式得
, 代入
式得
,
可知,是
的函数,自变量
的取值范围是
.
根据函数解析式 , 按照如表中自变量
的值计算
精确到个位
, 得到了
与
的几组对应值:
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点;
半径为
的圆柱形容器比半径为
的圆柱形容器表面积
填“大”或“小”
;
若容器的表面积为
, 容器底面半径约为
精确到
.
例如:节目演出后各个评委所给分数如表:
评委编号 | ||||||||||
评分 |
评分方案如下:
方案一:取各位评委所给分数的平均数则该节目的得分为 .
方案二:从评委所给的分数中先去掉一个最高分和一个最低分,再取其余八位评委所给分数的平均数,则该节目的得分为
回答下列问题:
如当时,则
.
该节目的得分为 .
Ⅰ当按照“方案三”中
评分时,
节目的得分为.
Ⅱ关于评分方案,下列说法正确的有.
当
时,
节目按照“方案三”和“方案一”评分结果相同;
当
时,说明“方案三”评分更注重节目的专业性;
当
时,
节目按照“方案三”评分的结果比“方案一”和“方案二”都高.
若
的最小值是
, 求
的最大值;
若对于
,
, 都有
, 求出
的取值范围.
求证:
;
求证:
;