题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广东省阳江市阳东区2023-2024学年七年级下学期数学期中...

更新时间：2024-05-22 浏览次数：19 类型：期中考试

一、选择题（本题共10小题，每小题3分，共30分）

1. (2024七下·阳东期中) 在实数 $\text{[math]}$ ， $\text{[math]}$ ， 0， $\text{[math]}$ 中，最小的数是（）

A . $\text{[math]}$ B . 0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·阳东期中) 8的立方根是（）

A . 2 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·阳东期中) 下列各点中，在第二象限的是（）

A . (5，3) B . (－5，0) C . (－5，1) D . (－5，－1)

答案解析收藏纠错 + 选题
4. (2024七下·阳东期中) 下列选项中， $\text{[math]}$ 与 $\text{[math]}$ 是对顶角的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024七下·阳东期中) 如下是小佳的练习册，她答对的题目数量是（）
判断题：
1． $\text{[math]}$ 一定没有平方根（√）
2． $\text{[math]}$ 的平方根是 $\text{[math]}$ （×）
3.25的平方根是5（×）
4.6是36的一个平方根（√）

A . 1道 B . 2道 C . 3道 D . 4道

答案解析收藏纠错 + 选题
6. (2024七下·阳东期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·阳东期中) 在平面内，将一个直角三角板按如图所示摆放在一组平行线上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 35° B . 40° C . 45° D . 50°

答案解析收藏纠错 + 选题
8. (2024七下·阳东期中) 如图，线段 $\text{[math]}$ 经过平移得到线段 $\text{[math]}$ ，其中点A ， B、 $\text{[math]}$ ，这四个点都在格点上．若线段 $\text{[math]}$ 上有一个点 $\text{[math]}$ ，则点P在 $\text{[math]}$ 上的对应点 $\text{[math]}$ 的坐标为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024七下·阳东期中) 如图，已知线段 $\text{[math]}$ ， $\text{[math]}$ 的长度分别是1， $\text{[math]}$ ，以原点为圆心，分别以 $\text{[math]}$ ， $\text{[math]}$ 的长为半径画弧，与数轴负半轴相交，交点对应的数字分别记为a ， b ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·阳东期中) 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为 $\text{[math]}$ ， $\text{[math]}$ ，若CD∥BE ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（共6小题，每小题3分，共18分）

11. (2024七下·徐汇期末) 比较大小： $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024七下·阳东期中) 在平面直角坐标系中，若点 $\text{[math]}$ 满足 $\text{[math]}$ ，则点A的坐标可以是（写出一个即可）

答案解析收藏纠错 + 选题
13. (2024七下·阳东期中) “在同一平面内，若a⊥b， $\text{[math]}$ ，则 $\text{[math]}$ ”，这是一个命题．（填“真”或“假”）

答案解析收藏纠错 + 选题
14. (2024七下·阳东期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024七下·阳东期中) 如图所示，△OAB的顶点B的坐标为（4，0），把△OAB沿x轴向右平移得到△CDE，如果CB＝1，那么OE的长为．

答案解析收藏纠错 + 选题
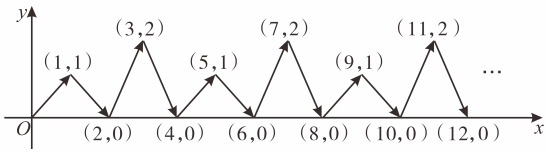
16. (2024七下·阳东期中) 如图，点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2）……，按这样的运动规律，经过第2025次运动后动点P的坐标是．

答案解析收藏纠错 + 选题

三、解答题（一）（共4小题，其中第17、18每小题各4分，第19、20每小题各6分，共20分）

17. (2024七下·阳东期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024七下·阳东期中) 已知点 $\text{[math]}$ ，若点M在第四象限，且到x轴，y轴的距离相等，求点M的坐标．

答案解析收藏纠错 + 选题
19. (2024七下·阳东期中) 请将下面的证明过程补充完整．
已知：如图， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．
证明：∵ $\text{[math]}$ ．
∴ $\text{[math]}$ ．
…

答案解析收藏纠错 + 选题
20. (2024七下·阳东期中) 如图是一个数值转换器，请根据其原理解决问题：当x为12时，求y的值，并写出详细过程．

答案解析收藏纠错 + 选题

四、解答题（二）（共3小题，其中第21题8分，第22、23每小题各10分，共28分）

21. (2024七下·阳东期中) 已知实数x ， y满足关系式 $\text{[math]}$ ．（x ， y均大于0）
1. （1）求x ， y的值；
2. （2）判断x和y的大小关系，并说明理由．
答案解析收藏纠错 + 选题
22. (2024七下·阳东期中) 如图，在平面直角坐标系中，已知三角形 $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将三角形 $\text{[math]}$ 先向右平移3个单位长度，再向下平移4个单位长度得到三角形 $\text{[math]}$ ．
1. （1）画出三角形 $\text{[math]}$ ，并写出点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标；
2. （2）若点 $\text{[math]}$ 是三角形 $\text{[math]}$ 内部的一点，经过平移后对应点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，求m和n的值．
答案解析收藏纠错 + 选题
23. (2024七下·阳东期中) 如图，在三角形 $\text{[math]}$ 中，D ， E是 $\text{[math]}$ 上的点，F是 $\text{[math]}$ 上一点，H ， G是 $\text{[math]}$ 上的点， $\text{[math]}$ 于点D ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．给定三个条件：① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ ．
1. （1）请在上述三个条件中选择其中两个作为已知条件．另一个作为结论组成一个真命题，你选择的条件是．结论是（填写序号）；
2. （2）证明上述命题．
答案解析收藏纠错 + 选题

五、解答题（三）（共2小题，每小题12分，共24分）

24. (2024七下·阳东期中) 已知点 $\text{[math]}$ ，将线段 $\text{[math]}$ 平移至线段 $\text{[math]}$ （A的对应点是点B）， $\text{[math]}$ ． a是 $\text{[math]}$ 的算术平方根， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，正数b满足 $\text{[math]}$ ．
1. （1）分别求出a、m、n、b的值；
2. （2）求A ， B ， C三点坐标；
3. （3）如图，若 $\text{[math]}$ ，点P为y轴正半轴上一动点，试探究 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系．（用含 $\text{[math]}$ 的式子表示）
答案解析收藏纠错 + 选题
25. (2024七下·阳东期中) 综合与实践：综合与实践活动课上，孙老师让同学们以“奇妙的平行线”为主题开展数学活动．如图1， $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别在射线 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ =度；探究中小聪同学发现，过点 $\text{[math]}$ 作 $\text{[math]}$ 即可得到 $\text{[math]}$ 的度数，请直接写出 $\text{[math]}$ 的度数；
2. （2）小明同学发现：无论 $\text{[math]}$ 如何变化， $\text{[math]}$ 的值始终为定值，并给出了一种证明该发现的辅助线作法：如图2，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于 $\text{[math]}$ ，请你根据小明同学提供的辅助线，先确定该定值，并说明理由；
3. （3）如图3，把“ $\text{[math]}$ ”改为“ $\text{[math]}$ ” （ $\text{[math]}$ ），其它条件保持不变，猜想 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
答案解析收藏纠错 + 选题

试卷信息