一、选择题:(本大题共10题,每题3分,共30分.)
-
-
-
-
A . 六边形
B . 七边形
C . 八边形
D . 九边形
-
-
-
7.
(2024八下·金东期中)
甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均数及方差如表所示,要选一个成绩较好且稳定的运动员去参赛,应选运动员( )
A . 甲
B . 乙
C . 丙
D . 丁
-
8.
(2024八下·金东期中)
为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为
x , 则下面所列方程正确的是( )
-
9.
(2024八下·金东期中)
如图,在

中,点

是线段

上一动点,过点

作

, 当点

从点

向点

运动过程中,四边形

的面积的变化情况是( )

A . 保持不变
B . 一直减小
C . 一直增大
D . 先增大后减小
-
10.
(2024八下·金东期中)
如图,

的对角线

交于点

平分
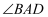
, 交

于点
E , 且

,

, 连接

, 下列结论:①

;②

;③

;④

, 其中成立的个数为( )

A . 1个
B . 2个
C . 3个
D . 4个
二、填空题:(本大题共6题,每题4分,共24分.)
-
-
12.
(2024八下·金东期中)
如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB的中点M,N,测得MN=16m,则A,B两点间的距离是
m.

-
-
-
15.
(2024八下·金东期中)
对于两个互不相等的有理数
a ,
b我们规定符号

表示
a ,
b两个数中最大的数.按照这个规定则方程

的解为
.
-
三、解答题:(本大题共8题,共66分.解答应写出文字说明,证明过程或演算步骤.)
-
-
(1)

-
(2)

-
-
(1)

-
(2)

-
19.
(2024八下·金东期中)
某班进行“闪亮之星”的推选工作,经过自荐和第一轮筛选后,甲、乙两位同学进入终选.如表为甲、乙两位同学的得分情况.其中人气分的计算方法是:根据班级主科老师和同学的投票结果,老师一票记10分,同学一票记2分,两个分数相加即为人气分.
学生 | 人气分 | 学习分 | 行规分 | 工作分 |
老师票数 | 同学票数 | 分数 |
甲 | 4 | 20 | a | 85 | 95 | 85 |
乙 | b | 25 | 70 | 90 | 92 | 90 |
-
(1)

,

;
-
(2)
经全班同学讨论决定,将人气、学习、行规、工作四个方面在总分中所占的比例分别为20%,25%,30%,25%.经计算,甲同学的最终得分为87分,请你求出乙同学的最终得分,并判断哪位同学当选.
-
-
(1)
请在图中作出点
A关于点
B的对称点

, 并求出

的坐标.
-
(2)
若点C与原点重合,以A、B、C、D四点为顶点的四边形为平行四边形,则点D的坐标为.
-
(3)
若
C点在直线

上运动,以
A、
B、
C、
D四点为顶点的四边形为平行四边形,则线段

的最小值为
.
-
-
(1)
求证:

.
-
(2)
若

, 求

的长;
-
(3)
点
F为

的中点,连接

, 交

于点
G , 求证:

.
-
22.
(2024八下·金东期中)
一些含根号的式子可以写成另一个式子的平方,如

.
设 (其中a、b、m、n均为正整数),则有
(其中a、b、m、n均为正整数),则有 , 这样可以把部分
, 这样可以把部分 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照上述的方法探索并解决下列问题:
-
-
(2)
当
a、
b、
m、
n均为正整数时,若

, 用含
m、
n的式子分别表示
a、
b , 得:

,

.
-
(3)
化简

.
-
23.
(2024八下·金东期中)
如图,在四边形

中,

, 动点
M从点
B出发沿线段

以每秒1个单位长度的速度向终点
C运动;同时动点
N从点
D出发沿线段

向终点
B运动.设运动的时间为
t秒.

备用图
-
(1)
直接写出

(用含
t的代数式表示),

.
-
(2)
如果当四边形

是平行四边形时,点
M与点
N恰好相遇,求点
N的运动速度;
-
(3)
在(2)的条件下,求出t为何值时,以点A、M、N、D为顶点的四边形是平行四边形.
 B .
B .  C .
C .  D .
D . 

(其中a、b、m、n均为正整数),则有
, 这样可以把部分
的式子化为平方式的方法.