 B .
B .  C .
C .  D .
D . 
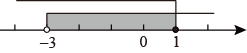 B .
B . 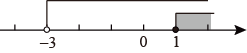 C .
C . 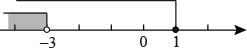 D .
D . 方案A.
方案B.
方案C.(D为BC的中点)
方案D.(O为
三边的垂直平分线的交点)
四种方案中光缆铺设路线最短的是( )
 B .
B .  C .
C .  D .
D . 


已知关于x的方程 .
背景 | 亚运会期间,小明所在的班级开展知识竞赛,需要去商店购买 | |
素材1 | 某商店在无促销活动时,若买15个 |
|
素材2 | 该商店龙年迎新春促销活动:用35元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折出售(已知小明在此之前不是该商店的会员); 线上淘宝店促销活动:购买商店内任何商品,一律按商品价格的9折出售且包邮. | |
问题解决 | ||
任务1 | 某商店在无促销活动时,求 | |
任务2 | 小明计划在促销期间购买A、B两款盲盒共40个,其中A款盲盒 若在线下商店购买,共需要 ▲ 元; 若在线上淘宝店购买,共需要 ▲ 元.(均用含 | |
任务3 | 请你帮小明算一算,在任务2的条件下,购买A款盲盒的数量在什么范围内时,线下购买方式更合算? | |
①如图2,当点D , E在直线BC右侧时,若 , 求
的度数;
②设(
),请直接用含
的式子表示
.
在中,
, 直线MN经过点A ,
于点D ,
于点E . 如图1,当直线MN在
外部时,称
和
是
的“双外弦三角形”,如图2,当直线MN在
内部时,称
和
是
的“双内弦三角形”,依据“两角及其夹边分别相等的两个三角形全等”的基本事实,我们得到“双外弦三角形”和“双内弦三角形”都是全等三角形,即
.

如图3,在中,
于点M ,
, E是BC边上的点,
,
, 连接AD , BD , 若
, 求BD的长.
小亮同学在阅读与理解【概念建构】的基础上,作于点N构造出如图4所示的“双内弦三角形”,并应用“双内弦三角形”是全等三角形的结论求出了BD . 请你依照小亮的解题思路,写出解答过程.
如图5,在中,
, D是AB边上一点,
, DE交BC于点N , 延长EB , CD交于点F , 猜想DB , DF , CN之间的数量关系,并说明理由.
如图6, ,
和
是等腰直角三角形,
,
, 直接写出
和
的面积和.
如图7,在中,
, 点D在AB边上,过B作
交CD延长线于点E , 延长EB至点F , 连接CF , 使
, 连接AF交CD于点G , 若
, 直接写出
的面积.