一、选择题:(本题有10小题,每小题3分,共30分)
-
-
-
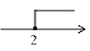
3.
已知实数a,b,若

, 则下列结论正确的是( )
-
-
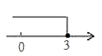
5.
下列命题是假命题的是( )
A . 直角三角形中,30°角所对的直角边等于斜边的一半
B . 有两个角相等的三角形是等腰三角形
C . 三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等
D . 三角形的角平分线将三角形分成面积相等的两部分
-
A . ①②
B . ②③
C . ①③
D . ②④
-
A . 10°
B . 15°
C . 20°
D . 25°
-
8.
(2024八下·罗湖期中)
如图,在

中,

,

,
BC边的垂直平分线交
AB于
E , 交
BC于点
D , 若

, 则

的周长为( )

A . 12
B . 14
C . 16
D . 19
-
-
10.
(2024八下·罗湖期中)
如图,
O是等边

内一点,

,

,

, 将线段
BO以点
B为旋转中心逆时针旋转60°得到线段

, 则

的度数为( )

A . 100°
B . 120°
C . 130°
D . 150°
二、填空题:(本题共5小题,每小题3分,共15分)
-
-
12.
如果将点

向右平移2个单位长度,再向下平移3个单位得到点
B , 那么点
B的坐标是
.
-
13.
某次知识竞赛共有20道选择题,规定答对一道题得10分,答错或不答一道题扣3分,若小刚希望总得分不少于70分,则他至少需答对道题.
-
14.
(2024八下·罗湖期中)
如图,在

中,

,

,

绕点
A按逆时针方向旋转到

的位置,点
D在
BC边上,
DE交
AC于点
F , 则

.

-
15.
(2024八下·罗湖期中)
如图,三角形纸片中,

,

,

, 折叠这个三角形,使点B落在

的中点D处,折痕为

, 那么

的长为
.

三、解答题:(共7小题,其中第16题6分,第17题6分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分,共55分)
-
-
-
(1)
请你画出

向左平移5个单位长度后得到的

;
-
(2)
请你画出

关于原点对称的

;
-
(3)
在
x轴上求作一点
P , 使

的周长最小,此时点
P的坐标为
.
-
-
(1)
若

, 求出

的度数;
-
(2)
若

周长为14cm,

, 求
DC的长.
-
-
(1)
分析:对不等式

来说,把

和

看成两个数
a和
b , 所以按照上述原理可知:(Ⅰ)

或(Ⅱ)

,
所以不等式 的求解就转化为求解不等式组(Ⅰ)和(Ⅱ),请你按照此种方法求出不等式
的求解就转化为求解不等式组(Ⅰ)和(Ⅱ),请你按照此种方法求出不等式 的解集;
的解集;
-
(2)
应用:解不等式

.
-
20.
用甲乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
原料 | 甲种原料 | 乙种原料 |
维生素C含量(单位/kg) | 500 | 200 |
原料价格(元/kg) | 8 | 4 |
现配制这种饮料10kg,要求至少含有4100单位的维生素C,设购买甲种原料x千克.
-
-
(2)
设用于购买这两种原料的总费用不超过76元时,则x在什么范围内才符合要求?
-
-
(1)
请你完成下列步骤,并画出函数

的图象.
①列表:
②描点;
③连线.
-
(2)
观察图象,当x1时(填“>”,“<”或“=”),y随x的增大而减小;
-
(3)
根据图象,不等式

的解集为
.
-
-
(1)
问题背景:如图,在等腰直角

中,点
C是
AB边上的中点,点
D是
OA上一点,连接
DC并延长至点
E , 使得

, 连接
BE , 请证明:

;
-
(2)
迁移应用:如图2,

和

均为等腰直角三角形,

,

, 将

绕点
B旋转,连接
AC , 点
E为
AC中点,连接
OE、
DE , 请你判断
OE与
DE的数量关系以及位置关系,并证明.
-
(3)
拓展延伸:如图3,将(2)中等腰直角

换成等腰直角

,

, 将

绕点
O旋转,连接
AC ,
BD , 点
E为
BD中点,连接
OE , 当点
A、
C、
D三点共线时,若

,

, 请你求出线段
OE的长.
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C . 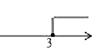 D .
D .