一、选择题(共10个小题,每小题3分,满分30分)
-
-
A . 5,11,12
B . 2, ,
,  C .
C .  ,
,  ,
,  D . 9,12,15
D . 9,12,15
-
-
-
-
-
A . OA=OC , OB=OD
B . AB=CD , AO=CO
C . AB=CD , AD=BC
D . ∠BAD=∠BCD , AB∥CD
-
-
A . 对角线相等
B . 对角线互相平分
C . 对角线平分一组对角
D . 对角线互相垂直
-
10.
(2024九上·高州月考)
如图,

,

,

和

都是等边三角形,
F为
AB中点,
DE交
AB于
G点,下列结论中,正确的结论有( )个
① ;②四边形ADFE是菱形;
;②四边形ADFE是菱形;
③ ;④
;④ .
.

A . 1
B . 2
C . 3
D . 4
二、填空题(共5个小题,每小题3分,满分15分)
-
-
-
13.
(2024八下·徐闻期中)
如图所示的一块地,∠ADC=90°,CD=3,AD=4,AB=13,BC=12,求这块地的面积为
.

-
14.
(2024八下·徐闻期中)
如图,数轴上,
O为原点,点
A表示-2,过点
A作

, 使

;再以
O为圆心,
OB的长为半径作弧,交数轴正半轴于点
P , 那么点
P表示的数是
.

-
15.
(2024八下·徐闻期中)
如图,菱形
ABCD周长为16,

,
E是
AB的中点,
P是对角线
AC上的一个动点,则

的最小值是
.

三、解答题(一)(共3个小题,每小题8分,满分24分)
四、解答题(二)(共3个小题,每小题9分,满分27分)
-
-
(1)
求
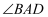
的度数.
-
-
-
-
(2)
若

,

, 求
BF的长.
-
-
(1)
具体运算,发现规律.

,

,

,

, 则

.
-
(2)
观察、归纳,猜想若n为正整数,用含n的式子表示上述的运算规律为:.
-
(3)
应用运算规律,求

的值.
五、解答题(三)(共2个小题,每小题12分,满分24分)
-
22.
(2024八下·徐闻期中)
问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小明想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

-
(1)
操作发现:小明在图1中画出

, 其顶点
A ,
B ,
C都是格点,同时构造正方形
BDEF , 使它的顶点都在格点上,且它的边
DE ,
EF分别经过点
C ,
A , 他借助此图求出了

的面积.在图1中,小明所画的

的三边长分别是

,

,

;

的面积为
.
-
(2)
解决问题:已知

中,

,

,

, 请你根据小明的思路,在图2的正方形网格中画出

, 并直接写出

的面积.
-
23.
(2024八下·徐闻期中)
如图,在四边形
ABCD中,

,

,

, 动点
P从点
B出发,沿射线
BC的方向以每秒3个单位的速度运动,动点
Q从点
A出发,在线段
AD上以每秒1个单位的速度向点
D运动,点
P、
Q分别从点
B、
A同时出发,当点
Q运动到点
D时,点
P随之停止运动,设运动时间为
t(秒).

-
-
-
(3)
是否存在以Q、D、C、P为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.



