江西省赣州市瑞金市2023-2024学年八年级下学期数学期中...

更新时间：2024-07-16 浏览次数：8 类型：期中考试

一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确选项．）

1. (2024八下·瑞金期中) 下列二次根式中，最简二次根式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·瑞金期中) 下列各组线段，能组成直角三角形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·瑞金期中) 如图，四边形ABCD的对角线交于点O ，下列哪组条件不能判断四边形ABCD是平行四边形（）

A . OA＝OC ， OB＝OD B . AB＝CD ， AO＝CO C . AB＝CD ， AD＝BC D . ∠BAD＝∠BCD ， AB∥CD

答案解析收藏纠错 + 选题
4. (2024八下·瑞金期中) 用四张一样大小的长方形纸片拼成一个如图所示的正方形 $\text{[math]}$ ，它的面积是75， $\text{[math]}$ ，图中空白的地方是一个正方形，那么这个小正方形的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·瑞金期中) 如图，一架2.5米长的梯子 $\text{[math]}$ 斜靠在墙 $\text{[math]}$ 上，这时梯足B到墙底端C的距离为0.7米，如果梯子的顶端沿墙垂直下滑0.4米，那么梯足将外移的长度是（）

A . 0.7米 B . 0.4米 C . 0.8米 D . 1米

答案解析收藏纠错 + 选题
6. (2024八下·瑞金期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ 是中线， $\text{[math]}$ 是角平分线， $\text{[math]}$ 于F ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 3 B . 1.5 C . 2 D . 2.5

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2024七下·全椒期末) 使 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
8. (2024八下·瑞金期中) 如图所示，四边形 $\text{[math]}$ 是平行四边形，点E在线段 $\text{[math]}$ 的延长线上，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2024八下·瑞金期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024八下·瑞金期中) 如图，在平行四边形 $\text{[math]}$ 中对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点O ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024八下·瑞金期中) 如图，某风景区的沿湖公路AB=3千米，BC=4千米，CD=12千米，AD=13千米，其中AB⊥BC ，图中阴影是草地，其余是水面．那么乘游艇游点C出发，行进速度为每小时11 $\text{[math]}$ 千米，到达对岸AD最少要用小时．

答案解析收藏纠错 + 选题
12. (2024九下·吉安模拟) 在△ABC 中，∠A=30°，∠B=90°，AC=8，点 D 在边 AB，且 BD= $\text{[math]}$ ，点 P 是△ABC 边上的一个动点，若 AP=2PD 时，则 PD的长是．

答案解析收藏纠错 + 选题

三、（本大题共5小题，每小题6分，共30分）

13. (2024八下·瑞金期中) 计算：
1. （1） $\text{[math]}$
2. （2）如图，在平行四边形 $\text{[math]}$ 中，点E、F分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是平行四边形
答案解析收藏纠错 + 选题
14. (2024八下·瑞金期中) 有一块矩形木板，木工采用如图的方式，在木板上截出两个面积分别为 $\text{[math]}$ 和 $\text{[math]}$ 的正方形木板.
1. （1）截出的两块正方形木料的边长分别为，.
2. （2）求剩余木料的面积.
答案解析收藏纠错 + 选题
15. (2024八下·瑞金期中) 如图，有一张四边形纸片 $\text{[math]}$ ， $\text{[math]}$ ．经测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离．
2. （2）求这张纸片的面积．
答案解析收藏纠错 + 选题
16. (2024八下·瑞金期中) 已知四边形ABCD是平行四边形，BD为对角线，分别在图①、图②中按要求作图（保留作图痕迹，不写作法）．
1. （1）如图①，点P为AB上任意一点，请仅用无刻度的直尺在CD上找出另一点Q，使AP＝CQ；
2. （2）如图②，点P为BD上任意一点，请仅用无刻度的直尺在BD上找出一点Q，使BP＝DQ．
答案解析收藏纠错 + 选题
17. (2024八下·瑞金期中) 如图所示，在 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 中点，连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ，且当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

四、（本大题共3小题，每小题8分，共24分）

18. (2024八下·瑞金期中) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点O ，且E、F、G、H分别是 $\text{[math]}$ 的中点．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的周长．
答案解析收藏纠错 + 选题
19. (2024八下·瑞金期中)
1. （1）课本再现：
  如图1，四个全等的直角三角形拼成一个大正方形，中间空白部分也是正方形．已知直角三角形的两直角边长分别为a ， b ，斜边长为c ．课堂上，老师结合图形，用不同的方式表示大正方形的面积，证明了勾股定理，请证明： $\text{[math]}$ ．
2. （2）类比迁移：现将图1中的两个直角三角形向内翻折，得到图2，若 $\text{[math]}$ ， $\text{[math]}$ ，求空白部分的面积．
答案解析收藏纠错 + 选题
20. (2024八下·瑞金期中) 秦九韶（1208年~1268年），字道古，南宋著名数学家．与李冶、杨辉、朱世杰并称宋元数学四大家，他精研星象、音律、算术、诗词、弓剑、营造之学，他于1247年完成的著作《数学九章》中关于三角形的面积公式与古希腊几何学家海伦的成果并称“海伦−秦九韶公式”，它的主要内容是，如果一个三角形的三边长分别是a ， b ， c ，记 $\text{[math]}$ ， S为三角形的面积，那么 $\text{[math]}$ ．
1. （1）如图在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请用上面的公式计算 $\text{[math]}$ 的面积；
2. （2）一个三角形的三边长分别为a ， b ， c ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值，
答案解析收藏纠错 + 选题

五、（本大题共2小题，每小题9分，共18分）

21. (2024八下·瑞金期中) 如图所示，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 的角平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点F ，交 $\text{[math]}$ 的延长线于点E ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 恰好平分 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是平行四边形；
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求平行四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
22. (2024八下·瑞金期中) 定义：我们将 $\text{[math]}$ 与 $\text{[math]}$ 称为一对“对偶式”．因为 $\text{[math]}$ ，可以有效的去掉根号，所以有一些问题可以通过构造“对偶式”来解决．
例如：已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值，可以这样解答：
因为 $\text{[math]}$ ，
所以 $\text{[math]}$ ．
1. （1）已知： $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）结合已知条件和第①问的结果，解方程： $\text{[math]}$ ；
3. （3）计算： $\text{[math]}$ ．
答案解析收藏纠错 + 选题

六、（本大题共12分）

23. (2024八下·瑞金期中) 综合与实践；
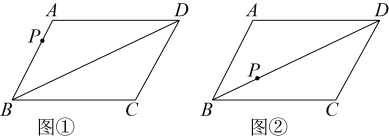
【问题情境】为了研究折纸过程中蕴涵的数学知识，老师发给每位同学完全相同的纸片，纸片形状如图1，在四边形 $\text{[math]}$ 中（ $\text{[math]}$ ）， $\text{[math]}$ ， $\text{[math]}$ ．
【探究实践】
老师引导同学们在边 $\text{[math]}$ 上任取一点E ，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，点C的对应点为H ，然后将纸片展平，连接 $\text{[math]}$ 并延长，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点M ， G ．老师让同学们探究：当点E在不同位置时，能有哪些发现？经过思考和讨论，小莹、小明向同学们分享了自己的发现．
1. （1）如图2，小莹发现：“当折痕 $\text{[math]}$ 与 $\text{[math]}$ 夹角为 $\text{[math]}$ 时，则四边形 $\text{[math]}$ 是平行四边形”．请你判断小莹的结论是否正确，并说明理由．
2. （2）如图3，小明发现：“当E是 $\text{[math]}$ 的中点时，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点N ，连接 $\text{[math]}$ ，则N是 $\text{[math]}$ 的中点”，请你判断小明的结论是否正确，并说明理由．
3. （3）【拓展应用】
  如图4，小慧在小明发现的基础上，经过进一步思考发现：“延长 $\text{[math]}$ 交 $\text{[math]}$ 于点F ．当给出 $\text{[math]}$ 和 $\text{[math]}$ 的长时，就可以求出 $\text{[math]}$ 的长”．老师肯定了小慧同学结论的正确性．若 $\text{[math]}$ ， $\text{[math]}$ ，请你帮小慧求出 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题