一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。
-
-
A . 20
B . 30
C . 42
D . 56
-
A . 40
B . 120
C . 121
D . 363
-
4.
(2024高二下·广州期中)
已知射击运动员甲击中靶心的概率为0.8，射击运动员乙击中靶心的概率为0.9，且甲、乙两人是否击中靶心互不影响．若甲、乙各射击一次，则至少有一人击中靶心的概率为（ ）
A . 0.98
B . 0.8
C . 0.72
D . 0.26
-
-
6.
(2024高二下·广州期中)
为展示六和课程的课程理念和实施成果，协和学校计划在篮球场和中心广场各布置一个六和课程多元文化展板，由甲、乙在内的5名学生志愿者协助布置，每人参与且只参与一个展板的布置，每个展板都至少由两人安装，若甲和乙必须安装不同的展板，则不同的分配方案种数为（ ）
A . 8
B . 10
C . 12
D . 14
-
7.
(2024高二下·广州期中)
已知椭圆
C：
＝1的上顶点为
P ， 左焦点为
F ， 直线
PF与
C的另一个交点为
Q ， 若|
PF|＝3|
QF|，则
C的离心率
e＝（ ）
-
二、多选题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分。
-
A . a3＝160
B . a1+a2+a3+a4+a5+a6＝0
C . 此二项式展开式的二项式系数和为64
D . 此二项式系数最大项为第4项
-
10.
(2024高二下·广州期中)
已知抛物线
y2＝2
px（
p＞0）的焦点为
F ， 点
P（5，
y0）在抛物线上，且|
PF|＝6，过点
P作
PQ⊥
x轴于点
Q ， 则（ ）
A . p＝2
B . 抛物线的准线为直线y＝﹣1
C . 
D . △FPQ的面积为
-
11.
(2024高二下·广州期中)
如图所示，从一个半径为
（单位：
m）的圆形纸板中切割出一块中间是正方形，四周是四个正三角形的纸板，以此为表面（舍弃阴影部分）折叠成一个正四棱锥
P﹣
ABCD ， 则以下说法正确的是（ ）
A . 四棱锥P﹣ABCD的体积是
m3
B . 四棱锥P﹣ABCD的外接球的表面积是8πm2
C . 异面直线PA与CD所成角的大小为60°
D . 二面角A﹣PB﹣C所成角的余弦值为
三、填空题：本题共3小题，每小题5分，共15分
-
-
13.
(2024高二下·广州期中)
某校面向高一全体学生共开设3门体育类选修课，每人限选一门．已知这三门体育类选修课的选修人数之比为6：3：1，考核优秀率分别为20%、16%和12%，现从该年级所有选择体育类选修课的同学中任取一名，其成绩是优秀的概率为
．
-
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤。
-
-
-
（2）
记
， 数列{
bn}的前
n项和为
Sn ， 证明：
．
-
16.
(2024高二下·广州期中)
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
-
-
-
（3）
设ξ为取出的4个球中红球的个数，求ξ的分布列．
-
17.
(2024高二下·广州期中)
在四棱锥
P﹣
ABCD中，底面
ABCD为等腰梯形，平面
PAD⊥底面
ABCD ， 其中
AD∥
BC ，
AD＝2
BC＝4，
AB＝3，
PA＝
PD＝2
， 点
E为
PD中点．
-
-
-
-
-
（2）
证明：当
a＞0时，
．
-
-
-
（2）
点A ， B ， D是双曲线C上不同的三点，且B ， D两点关于y轴对称，△ABD的外接圆经过原点O ． 求证：点A与点B的纵坐标互为倒数；
-
（3）
在（2）的条件下，试问是否存在一个定圆与直线AB相切，若有，求出定圆方程，没有说明理由．
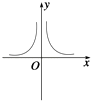B . 
C . 
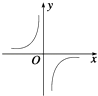D . 
