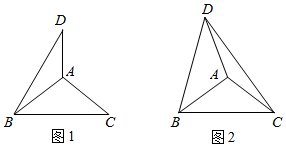
A.如图1,将线段绕点B逆时针旋转
得到线段
, 连接
, 则
的长为.
B.如图2,将线段绕点B逆时针旋转得到线段
, 连接
,
, 若
, 则
的长为.
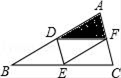

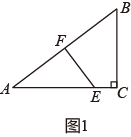

A.如图1,AB边的垂直平分线交AC于点E,交AB于点F.若AE=5,EF=3,则线段EC的长为;
B.如图2,∠ABC的平分线交AC于点D,AB边的垂直平分线交AC于点E,AC=8,BC=6,线段DE的长为.
注:如果选择多个条件分别解答,按第一个解答计分.

已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,(填写序号).
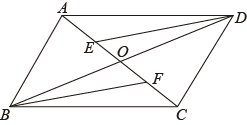
求证:四边形DEBF是平行四边形.

如图, 分别是梯形
的两腰
和
的中点,即
为梯形
的中位线.请同学们思考梯形的中位线与两底有何数量关系与位置关系?并给予证明.

猜想:
已知:
求证:
证明:
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,(填写序号).
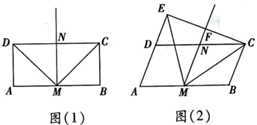
数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.
小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
问题情境:学习完平行四边形的性质和判定后,老师创设了如下探究情境,探究三角形的中位线定理.
问题1:如图1,在中,对角线AC,BD相交于点O,E为AB上一点,连接EO并延长交CD于F,则OE与OF有怎样的数量关系?

小明: .
理由如下:∵四边形ABCD是平行四边形,
∴ ,
(依据1)
∴
又∵ ,
∴(依据2).
∴
问题2:如图2,若点E为AB的中点,其他条件不变,则线段EF与BC有怎样的数量关系和位置关系?
小亮: ,
BC.
理由如下:….
问题3:如图3,在中,D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边中点的线段叫做三角形的中位线.通过前面问题给你的启发,你能猜想出DE和BC的数量关系和位置关系吗?
小慧:BC,
.
…
数学思考:
依据1:;依据2:.
请用图3写出三角形中位线定理的证明过程.