四川省遂宁市射洪市2023-2024学年高三下学期高考模拟测...

更新时间：2024-06-24 浏览次数：14 类型：高考模拟

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．

1. (2024高三下·射洪模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高三下·射洪模拟) 复数 $\text{[math]}$ （ $\text{[math]}$ 是虚数单位）在复平面内对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024高三下·射洪模拟) 某学校为了解1 000名新生的身体素质，将这些学生编号为1，2，…，1 000，从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到，则下面4名学生中被抽到的是（）

A . 815号学生 B . 616号学生 C . 200号学生 D . 8号学生

答案解析收藏纠错 + 选题
4. (2024高三下·射洪模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高三下·射洪模拟) 设 $\text{[math]}$ 是两条不同的直线， $\text{[math]}$ 是三个不同的平面，下列说法中正确的序号为（）
①若 $\text{[math]}$ ，则 $\text{[math]}$ 为异面直线 ②若 $\text{[math]}$ ，则 $\text{[math]}$
③若 $\text{[math]}$ ，则 $\text{[math]}$ ④若 $\text{[math]}$ ，则 $\text{[math]}$

A . ①② B . ③④ C . ②④ D . ②③

答案解析收藏纠错 + 选题
6. (2024高三下·射洪模拟) 在 $\text{[math]}$ 中，点F为线段BC上任一点（不含端点），若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 4 B . 8 C . 9 D . 2

答案解析收藏纠错 + 选题
7. (2024高三下·射洪模拟) 已知函数 $\text{[math]}$ 是R上的奇函数，且在 $\text{[math]}$ 上单调递减，若 $\text{[math]}$ ，则满足不等式 $\text{[math]}$ 的 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高三下·射洪模拟) 函数 $\text{[math]}$ ，（其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）其图象如图所示，为了得到 $\text{[math]}$ 的图象，可以将 $\text{[math]}$ 的图象（）

A . 向右平移 $\text{[math]}$ 个单位长度 B . 向左平移 $\text{[math]}$ 个单位长度 C . 向左平移 $\text{[math]}$ 个单位长度 D . 向右平移 $\text{[math]}$ 个单位长度

答案解析收藏纠错 + 选题
9. (2024高三下·射洪模拟) 设 $\text{[math]}$ 为双曲线 $\text{[math]}$ 的左、右焦点，直线 $\text{[math]}$ 过左焦点 $\text{[math]}$ 且垂直于一条渐近线，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 的渐近线分别交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在第一象限，且 $\text{[math]}$ ，则双曲线 $\text{[math]}$ 的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高三下·射洪模拟) 在一个半径为2的半球形封闭容器内放入两个半径相同的小球，则这两个小球的表面积之和最大为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高三上·成都月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高三下·射洪模拟) 设 $\text{[math]}$ 为坐标原点， $\text{[math]}$ 为椭圆 $\text{[math]}$ 的两个焦点， $\text{[math]}$ 两点在 $\text{[math]}$ 上，且 $\text{[math]}$ 关于坐标原点对称， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题共4小题，每小题5分，共20分．

13. (2024高三下·射洪模拟) 若 $\text{[math]}$ 满足约束条件 $\text{[math]}$ ，设 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
14. (2024高三下·射洪模拟) 从 $\text{[math]}$ 这五个数字中随机抽取两个数字组成一个两位数，则这个两位数是偶数的概率为．

答案解析收藏纠错 + 选题
15. (2024高三下·射洪模拟) 如图，有三座城市 $\text{[math]}$ ．其中 $\text{[math]}$ 在 $\text{[math]}$ 的正东方向，且与 $\text{[math]}$ 相距120 $\text{[math]}$ ； $\text{[math]}$ 在 $\text{[math]}$ 的北偏东30°方向，且与 $\text{[math]}$ 相距60 $\text{[math]}$ ．一架飞机从城市 $\text{[math]}$ 出发，沿北偏东75°航向飞行．当飞机飞行到城市 $\text{[math]}$ 的北偏东45°的D点处时，飞机出现故障，必须在城市 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中选择一个最近城市降落，则该飞机必须再飞行 $\text{[math]}$ ，才能降落．

答案解析收藏纠错 + 选题
16. (2024高三下·射洪模拟) 已知A，B为圆 $\text{[math]}$ 上的两个动点， $\text{[math]}$ ，若点P为直线 $\text{[math]}$ 上一动点，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每道试题考生都必须作答.第22、23题为选考题，考生根据要求作答.

17. (2024高三下·射洪模拟) 某保险公司为了给年龄在20～70岁的民众提供某种疾病的医疗保障，设计了一款针对该疾病的保险，现从10000名参保人员中随机抽取100名进行分析，这100个样本按年龄段[20，30），[30，40），[40，50），[50，60），[60，70]分成了五组，其频率分布直方图如下图所示，每人每年所交纳的保费与参保年龄如下表格所示．（保费：元）据统计，该公司每年为该项保险支出的各种费用为一百万元．
年龄 [20，30） [30，40） [40，50） [50，60） [60，70]
保费 x 2x 3x 4x 5x
1. （1）用样本的频率分布估计总体的概率分布，为使公司不亏本，则保费 $\text{[math]}$ 至少为多少元?（精确到整数元）
2. （2）经调查，年龄在 $\text{[math]}$ 之间的中年人对该疾病的防范意识还比较弱，为加强宣传，按分层抽样的方法从年龄在 $\text{[math]}$ 和 $\text{[math]}$ 的中年人中选取6人进行教育宣讲，再从选取的6人中随机选取2人，被选中的2人免一年的保险费，求被免去的保费超过150元的概率.
答案解析收藏纠错 + 选题
18. (2024高三下·射洪模拟) 已知等比数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 的通项公式，并求 $\text{[math]}$ 的值；
2. （2）令 $\text{[math]}$ ，设 $\text{[math]}$ 为数列 $\text{[math]}$ 的前n项和，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2024高三下·射洪模拟) 如图，在多面体ABCDEF中，四边形ABCD为菱形，AE＝2BF ， BF//AE ， BF⊥AD ，且平面ACE⊥平面ABCD.
1. （1）在DE上确定一点M ，使得FM//平面ABCD；
2. （2）若BF＝BA＝1，且 $\text{[math]}$ ，求多面体ABCDEF的体积.
答案解析收藏纠错 + 选题
20. (2024高三下·射洪模拟) 已知过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，抛物线在点 $\text{[math]}$ 处的切线为 $\text{[math]}$ ，在 $\text{[math]}$ 点处的切线为 $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，当直线 $\text{[math]}$ 的倾斜角为45°时， $\text{[math]}$ ．
1. （1）求抛物线 $\text{[math]}$ 的方程；
2. （2）设线段 $\text{[math]}$ 的中点为 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
21. (2024高三下·射洪模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 为曲线 $\text{[math]}$ 与 $\text{[math]}$ 的一条公切线.
1. （1）求 $\text{[math]}$ ；
2. （2）若直线 $\text{[math]}$ 与曲线 $\text{[math]}$ ，直线 $\text{[math]}$ ，曲线 $\text{[math]}$ 分别交于 $\text{[math]}$ 三点，其中 $\text{[math]}$ ，且 $\text{[math]}$ 成等差数列，证明：满足条件的 $\text{[math]}$ 有且只有一个.
答案解析收藏纠错 + 选题

四、请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分.【选修4—4：坐标系与参数方程】

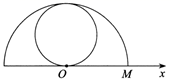
22. (2024高三下·射洪模拟) 如图，在极坐标系中，已知点 $\text{[math]}$ ，曲线 $\text{[math]}$ 是以极点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径的半圆，曲线 $\text{[math]}$ 是过极点且与曲线 $\text{[math]}$ 相切于点 $\text{[math]}$ 的圆.
1. （1）分别写出曲线 $\text{[math]}$ ， $\text{[math]}$ 的极坐标方程；
2. （2）直线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）与曲线 $\text{[math]}$ ， $\text{[math]}$ 分别相交于点 $\text{[math]}$ ， $\text{[math]}$ （异于极点），求 $\text{[math]}$ 面积的最大值.
答案解析收藏纠错 + 选题

五、【选修4—5：不等式选讲】

23. (2024高三下·射洪模拟) 已知函数 $\text{[math]}$ .
1. （1）求不等式 $\text{[math]}$ 的解集；
2. （2）若函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ ，正数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题