湖南省岳阳市临湘市2023-2024学年八年级下学期数学期中...

更新时间：2024-06-17 浏览次数：5 类型：期中考试

一、选择题。（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024八上·临湘期中) 下面的图形中，是中心对称图形的是（）

A . 等边三角形 B . 平行四边形 C . 直角三角形 D . 等腰梯形

答案解析收藏纠错 + 选题
2. (2024八上·临湘期中) 直角三角形的斜边长为10，则斜边上的中线长为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
3. (2024八下·临湘期中) 下满足下列条件时， $\text{[math]}$ 不是直角三角形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·临湘期中) 关于 $\text{[math]}$ 的叙述，正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ 是菱形 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ 是正方形 C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 是矩形 D . 若 $\text{[math]}$ ，则 $\text{[math]}$ 是正方形

答案解析收藏纠错 + 选题
5. (2024八下·临湘期中) 如图，在 $\text{[math]}$ 中，下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·临湘期中) 如图，分别以线段AB的两端点A，B为圆心，大于 $\text{[math]}$ AB长为半径画弧，在线段AB的两侧分别交于点E，F，作直线EF交AB于点O.在直线EF上任取一点P（不与O重合），连接PA，PB，则下列结论不一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·临湘期中) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 交于点O ， M、N分别为 $\text{[math]}$ 、 $\text{[math]}$ 的中点。若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 2 B . 4 C . 8 D . 16

答案解析收藏纠错 + 选题
8. (2024八下·临湘期中) 如图所示，在等腰直角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 于E。若 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为（）

A . 6 B . 8 C . 10 D . 12

答案解析收藏纠错 + 选题
9. (2024八下·临湘期中) 如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
10. (2024八下·临湘期中) 如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去．已知第一个矩形的面积为1，则第n个矩形的面积为(　　)

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题。（本题共8小题，每小题3分，满分24分）

11. (2024八下·临湘期中) 已知在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 。

答案解析收藏纠错 + 选题
12. (2024八下·临湘期中) 如图，禁令标志是交通标志中的一种，是对车辆加以禁止或限制的标志，如禁止通行、禁止停车、禁止左转弯、禁止鸣喇叭、限制速度、限制重量等。如图，该禁令标志的内角和是。

答案解析收藏纠错 + 选题
13. (2024九上·北京市开学考) 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为度。

答案解析收藏纠错 + 选题
14. (2024八下·临湘期中) 如图， $\text{[math]}$ ，要根据“ $\text{[math]}$ ”证明 $\text{[math]}$ ，应添加的直接条件是.

答案解析收藏纠错 + 选题
15. (2024八下·临湘期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为。

答案解析收藏纠错 + 选题
16. (2024八下·临湘期中) 矩形的一条对角线长为4 $\text{[math]}$ ，两条对角线组成的对顶角中，有一组是 $\text{[math]}$ ，则矩形的面积为。

答案解析收藏纠错 + 选题
17. (2024八下·临湘期中) 如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为°．

答案解析收藏纠错 + 选题
18. (2024八下·临湘期中) 如图： $\text{[math]}$ 是边长为3 $\text{[math]}$ 的等边三角形动点P、Q同时从A、B两点出发，分别沿 $\text{[math]}$ 、 $\text{[math]}$ 方向匀速移动，它们的速度都是1 $\text{[math]}$ ，当点P到达B时，P、Q两点停止运动，当点P到达B时，P、Q两点停止运动。设点P运动的时间为 $\text{[math]}$ 。当t为时， $\text{[math]}$ 是直角三角形。

答案解析收藏纠错 + 选题

三、解答题。（本题共8小题，满分66分，解答应写出文字说明，证明过程或演算步骤）

19. (2024八下·临湘期中) 一个多边形的内角和的度数是外角和的4倍多180，求这个多边形的边数。

答案解析收藏纠错 + 选题
20. (2024八下·临湘期中) 如图，连接四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是直角三角形；
2. （2）求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
21. (2024八下·临湘期中) 如图，DE 是△ABC 的中位线，延长CB，至点F ，使 $\text{[math]}$ ，连接BE ，DF .
1. （1）求证：四边形BEDF 是平行四边形.
2. （2）若 $\text{[math]}$ ，试判断△ABC 的形状，并说明理由.
答案解析收藏纠错 + 选题
22. (2024八下·临湘期中) 如图，把边长为2 $\text{[math]}$ 的等边三角形 $\text{[math]}$ 绕边 $\text{[math]}$ 的中点O旋转 $\text{[math]}$ ，得到 $\text{[math]}$ 。
1. （1）四边形 $\text{[math]}$ 是什么样的四边形？说明理由。
2. （2）求四边形 $\text{[math]}$ 的两条对角线的长度。
3. （3）求四边形 $\text{[math]}$ 的面积。
答案解析收藏纠错 + 选题
23. (2024八下·临湘期中) 如图，一艘轮船航行到B处时，测得小岛A在船的北偏东 $\text{[math]}$ 的方向，轮船从B处继续向正东方向航行20海里到达C处时，测得小岛A在船的北偏东 $\text{[math]}$ 的方向。（参考数据： $\text{[math]}$ ）
1. （1）若小岛A到这艘轮船航行路线 $\text{[math]}$ 的距离是 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）已知在小岛周围17海里内有暗礁，若轮船不改变航向继续向前行驶，试问轮船有无触礁的危险？
答案解析收藏纠错 + 选题
24. (2024八下·临湘期中) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 的高。
1. （1）求证： $\text{[math]}$ 垂直平分 $\text{[math]}$ 。
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长。
答案解析收藏纠错 + 选题
25. (2024八下·临湘期中)
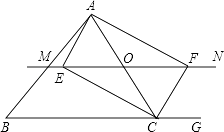
如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．
1. （1）试说明EO=FO；
2. （2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；
3. （3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．
答案解析收藏纠错 + 选题
26. (2024八下·临湘期中) 【问题呈现】
如图1， $\text{[math]}$ 的顶点在正方形 $\text{[math]}$ 两条对角线的交点处， $\text{[math]}$ ，将 $\text{[math]}$ 绕点P旋转，旋转过程中， $\text{[math]}$ 的两边分别与正方形 $\text{[math]}$ 的边 $\text{[math]}$ 和 $\text{[math]}$ 交于点E、F（点F与点C ， D不重合）。探索线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系。
1. （1）【问题初探】
  爱动脑筋的小悦发现，通过证明两个三角形全等，可以得到结论．请你写出线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由；
2. （2）【问题引申】
  如图2，将图1中的正方形 $\text{[math]}$ 改为 $\text{[math]}$ 的菱形， $\text{[math]}$ ，其他条件不变，请你帮小悦得出此时线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系是；
3. （3）【问题解决】
  如图3，在（2）的条件下，当菱形的边长为8，点P运动至与A点距离恰好为7的位置，且 $\text{[math]}$ 旋转至 $\text{[math]}$ 时， $\text{[math]}$ 的长度为。
答案解析收藏纠错 + 选题