江西省景德镇市乐平市2023-2024学年七年级下学期数学期...

更新时间：2024-07-25 浏览次数：4 类型：期中考试

一、单项选择题（本大题共有6小题，每题3分，共18分．）

1. (2024七下·新津月考) 下列运算正确的是（）

A . a²•a³=a⁶ B . （﹣a²）³=﹣a⁵ C . a¹⁰÷a⁹=a（a≠0） D . （﹣bc）⁴÷（﹣bc）²=﹣b²c²

答案解析收藏纠错 + 选题
2. (2024七下·乐平期中) 如图，下列结论正确的是（）

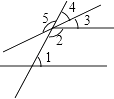
A . ∠5与∠2是对顶角 B . ∠1与∠3是同位角 C . ∠2与∠3是同旁内角 D . ∠1与∠2是同旁内角

答案解析收藏纠错 + 选题
3. (2024七下·乐平期中) 如图，已知直线 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·乐平期中) 如图所示，下列判断错误的是（）

A . 若∠1＝∠3，AD∥BC，则BD是∠ABC的平分线 B . 若AD∥BC，则∠1＝∠2＝∠3 C . 若∠3+∠4+∠C＝180°，则AD∥BC D . 若∠2＝∠3，则AD∥BC

答案解析收藏纠错 + 选题
5. (2024七下·乐平期中) 如图，点C在∠AOB的边OB上，用尺规作出了∠BCN=∠AOC，作图痕迹中，弧FG是（）

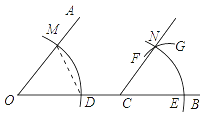
A . 以点C为圆心，OD为半径的弧 B . 以点C为圆心，DM为半径的弧 C . 以点E为圆心，OD为半径的弧 D . 以点E为圆心，DM为半径的弧

答案解析收藏纠错 + 选题
6. (2024七下·乐平期中) 小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还．”如果用纵轴y表示父亲与儿子行进中离家的距离，用横轴x表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题3分，共18分．）

7. (2024八上·朝阳月考) 若m、n满足 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. 已知 $\text{[math]}$ 是完全平方式，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
9. (2024七下·乐平期中) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2024七下·乐平期中) 某颗粒物的直径是0.000000071，把0.000000071用科学记数法表示为．

答案解析收藏纠错 + 选题
11. (2024七下·乐平期中) 如图， $\text{[math]}$ ，则 $\text{[math]}$ 度．

答案解析收藏纠错 + 选题
12. (2024七下·乐平期中) 已知王强家、体育场、学校在同一直线上，下面的图像反映的过程是：某天早晨，王强从家跑步去体育场锻炼，锻炼结束后，步行回家吃早餐，饭后骑自行车到学校．图中 $\text{[math]}$ 表示时间， $\text{[math]}$ 表示王强离家的距离．则下列结论正确的是．（填写所有正确结论的序号）
①体育场离王强家 $\text{[math]}$
②王强在体育场锻炼了 $\text{[math]}$
③王强吃早餐用了 $\text{[math]}$
④王强骑自行车的平均速度是 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题．（本大题有5小题，每小题6分，共30分）

13. (2024七下·乐平期中)
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$ （用简便方法计算）
答案解析收藏纠错 + 选题
14. (2024七下·乐平期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2024七下·乐平期中) 已知某长方形的面积是 $\text{[math]}$ ，它的一边长为 $\text{[math]}$ ，求此长方形的周长.

答案解析收藏纠错 + 选题
16. (2024七下·乐平期中) 如图，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在一条直线上， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2024七下·乐平期中) 草莓销售季节，某种植基地开发了草莓采摘无人销售方式，为方便小朋友体验，销售人员把销售的草莓数量x（kg）与销售总价y（元）之间的关系写在了下列表格中：
销售数量x（kg）
1
2
3
4
…
销售总价y（元）
8.5
16.5
24.5
32.5
…
1. （1）请你写出草莓的销售数量x（kg）与销售总价y（元）之间的关系式；
2. （2）丽丽一家共摘了6.5kg草莓，应付多少钱？
答案解析收藏纠错 + 选题

四、解答题．（本大题有3小题，每小题8分，共24分）

18. (2024七下·乐平期中) 若a、b可以代表一个数或一个代数式，定义运算“◎”如下： $\text{[math]}$
1. （1）化简：（2m）◎（3n）；
2. （2）若 $\text{[math]}$ ，求m ．
答案解析收藏纠错 + 选题
19. (2024七下·乐平期中) 填写下面解题过程中的推理依据：如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 吗？请说明理由．
  解： $\text{[math]}$ ，理由如下：
  因为 $\text{[math]}$ （已知），
  所以 $\text{[math]}$ （）．
  因为 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ （已知），
  所以 $\text{[math]}$ （角平分线的定义）， $\text{[math]}$ （角平分线的定义），
  所以 $\text{[math]}$ （）．
2. （2） $\text{[math]}$ 与 $\text{[math]}$ 的位置关系如何？为什么？
答案解析收藏纠错 + 选题
20. (2024七下·乐平期中) 泰和工农兵大道安装的护栏平面示意图如图所示，假如每根立柱宽为0.2米，立柱间距为3米．
1. （1）根据上图，将表格补充完整．
  立柱根数
  1
  2
  3
  4
  5
  ……
  护栏总长度（米）
  0.2
  3.4
  __
  9.8
  __
  ……
2. （2）在这个变化过程中，自变量、因变量各是什么？
3. （3）设有x根立柱，护栏总长度为y米，则y与x之间的关系式是什么？
4. （4）求护栏总长度为61米时立柱的根数？
答案解析收藏纠错 + 选题

五、解答题．（本大题有2小题，每小题9分，共18分）

21. (2024七下·乐平期中) 如图①是一个长为 $\text{[math]}$ 、宽为 $\text{[math]}$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形.
1. （1）请用两种不同的方法表示图②中阴影部分的面积（结果不化简）.
  方法1：；方法2：.
2. （2）观察图②，请写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个式子之间的等量关系；
3. （3）根据（2）题中的等量关系，解决如下问题：已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2024七下·乐平期中) 如图1，以直线 $\text{[math]}$ 上一点O为端点作射线 $\text{[math]}$ ，使 $\text{[math]}$ ．将一个直角三角板 $\text{[math]}$ 的直角顶点O放在直线 $\text{[math]}$ 上的点O处，边 $\text{[math]}$ 放在射线 $\text{[math]}$ 上．
1. （1） $\text{[math]}$ ；
2. （2）如图2，将直角三角板 $\text{[math]}$ 绕点O按逆时针方向转动，当射线 $\text{[math]}$ 恰好平分 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数；
3. （3）如图3，将直角三角板 $\text{[math]}$ 绕点O转动，如果 $\text{[math]}$ 始终在 $\text{[math]}$ 的内部，试猜想 $\text{[math]}$ 和 $\text{[math]}$ 有怎样的数量关系，并说明理由．
答案解析收藏纠错 + 选题

六、解答题．（本大题12分）

23. (2024七下·乐平期中) 求解下列各题
1. （1）如图（1）， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 外部，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$
2. （2）如图（2）， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 内部，则 $\text{[math]}$ 之间有何数量关系？证明你的结论；
3. （3）在图（2）中，将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转一定角度交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，如图（3），若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题