题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

湖南省初中学业水平考试2024年数学押题密卷（二）

更新时间：2024-06-17 浏览次数：1 类型：水平会考

一、选择题（在下列各题的四个选项中，只有一项是符合题意的. 请在答题卡中填涂符合题意的选项. 本大题共10个小题，每小题3分，共30分）

1. 下列实数中，负数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2024

答案解析收藏纠错 + 选题
2. (2024·湖南会考) 下列计算，结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·湖南会考) 下面四幅图分别是“故宫博物馆”“广东博物馆”、“四川博物馆”、“温州博物馆”的标志，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024·湖南会考) 某地自然风光秀丽，森林资源丰富，总面积约 $\text{[math]}$ 平方米．数据 $\text{[math]}$ 用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·湖南会考) 如图，已知直线a ， b被直线c所截，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·湖南会考) 已知一次函数表达式为： $\text{[math]}$ ，则此一次函数图象不经过第（）象限．

A . 一 B . 二 C . 三 D . 四

答案解析收藏纠错 + 选题
7. (2024·湖南会考) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2024·湖南会考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 的周长是（）

A . 20 B . 25 C . 28 D . 32

答案解析收藏纠错 + 选题
9. (2024·湖南会考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点A为圆心，适当长为半径作弧，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点D ， E ，再分别以点D ， E为圆心，大于 $\text{[math]}$ 长为半径作弧，两弧在 $\text{[math]}$ 的内部相交于点F ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点G ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积是（）

A . 24 B . 12 C . 10 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·湖南会考) 我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车，如图，筒车盛水桶的运行轨道是以轴心 $\text{[math]}$ 为圆心的圆，已知圆心 $\text{[math]}$ 在水面的上方， $\text{[math]}$ 的半径长为5米， $\text{[math]}$ 被水面截得的弦 $\text{[math]}$ 长为8米，点 $\text{[math]}$ 是运行轨道的最低点，则点 $\text{[math]}$ 到弦 $\text{[math]}$ 的距离为（）

A . 5米 B . 4米 C . 3米 D . 2米

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，共24分）

11. (2024·湖南会考) 分解因式： $\text{[math]}$ =

答案解析收藏纠错 + 选题
12. (2024九下·海淀模拟) 方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
13. (2024·湖南会考) 《九章算术》是中国古代数学专著，在数学上有其独到的成就，不仅最早提到了分数问题，原文如下：今有共买鸡，人出九；人出六，不足十六．问人数、鸡价各几何？译文为：现有若干人合伙出钱买鸡，如果每人出 $\text{[math]}$ 文钱，就会多 $\text{[math]}$ 文钱；如果每人出 $\text{[math]}$ 文钱，又会缺 $\text{[math]}$ 文钱，设合伙买鸡者有x人，鸡价为y文钱，可列方程组为．

答案解析收藏纠错 + 选题
14. (2024·湖南会考) 如图，反比例函数 $\text{[math]}$ 的图象过点A ，点A垂直于x轴，则 $\text{[math]}$ 的面积是．

答案解析收藏纠错 + 选题
15. (2024·湖南会考) 为了落实“双减”政策，增强学生体质，某校课后服务篮球兴趣课开展投篮比赛活动．其中8名选手投中篮圈的个数分别为 $\text{[math]}$ ，则这组数据的中位数是．

答案解析收藏纠错 + 选题
16. (2024·湖南会考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， E为 $\text{[math]}$ 中点，若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题
17. (2024·长沙模拟) 如图，点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，连接 $\text{[math]}$ ．若 $\text{[math]}$ 的半径为 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
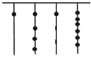
18. (2024·湖南会考) 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”.如图，一位妇女在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子出生后的天数为个.

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，第19、20题每小题6分，第21、22题每小题8分，第23、24题每小题9分，第25、26题每小题10分）

19. (2024·湖南会考) 计算： $\text{[math]}$ ；

答案解析收藏纠错 + 选题
20. (2024·湖南会考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024·湖南会考) 为了推进“优秀传统文化进校园”活动．宁蒗县某校准备在七年级成立四个课外活动小组，分别是：A ．民族舞蹈组；B ．经典诵读组；C ．民族乐器组；D ．民族歌曲组．为了解学生最喜欢哪一个活动小组，学校从九年级全体学生中随机抽取部分学生进行问卷调查，每人必须选择且只能选择一个小组，并将调查结果绘制成如图所示的两幅不完整的统计图．
请根据图中提供的信息，解答下列问题．
1. （1）本次调查的学生共有人，C中占扇形统计图中圆心角度数为度．
2. （2）在重阳节来临之际，学校计划组织学生到敬老院为老人表演节目，准备从这4个小组中随机抽取2个小组汇报演出，请你用列表法或画树状图法，求选中的2个小组恰好是C ， D小组的概率．
答案解析收藏纠错 + 选题
22. (2024·湖南会考) 如图，平地上建筑物 $\text{[math]}$ 与建筑物 $\text{[math]}$ 相距 $\text{[math]}$ ，在建筑物 $\text{[math]}$ 的顶部 $\text{[math]}$ 处测得建筑物 $\text{[math]}$ 顶部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，底部 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，求建筑物 $\text{[math]}$ 的高度．（结果保留整数．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
23. (2024·湖南会考) 现有某公司研发的一个新品种高产农作物，在研发第一阶段实现了亩产量400公斤的目标，第三阶段实现了亩产量2025公斤的目标．
1. （1）如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；
2. （2）按照（1）中亩产量增长率，科研团队期望在第四阶段实现亩产4500公斤的目标，请通过计算说明他们的目标能否实现．
答案解析收藏纠错 + 选题
24. (2024·湖南会考) 如图， $\text{[math]}$ 对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点O，过点D作 $\text{[math]}$ 且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2024九下·福田模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点D ，点E在 $\text{[math]}$ 上，以 $\text{[math]}$ 直径的 $\text{[math]}$ 经过点D ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若点F是劣弧 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，试求阴影部分的面积．
答案解析收藏纠错 + 选题
26. (2024·湖南会考) 如图，抛物线 $\text{[math]}$ 的顶点为A ，与y轴交于点C ．过点A作线段 $\text{[math]}$ 垂直y轴交于点B ，过点C作线段 $\text{[math]}$ 垂直抛物线的对称轴交于点D ，我们称矩形 $\text{[math]}$ 为抛物线 $\text{[math]}$ 的“伴随矩形”．
1. （1）请根据定义求出抛物线 $\text{[math]}$ 的“伴随矩形” $\text{[math]}$ 的面积；
2. （2）已知抛物线 $\text{[math]}$ 的“伴随矩形”为矩形 $\text{[math]}$ ，若矩形 $\text{[math]}$ 的四边与直线 $\text{[math]}$ 共有两个交点，且与双曲线 $\text{[math]}$ 无交点，请直接写出m的取值范围；
3. （3）若对于开口向上的抛物线 $\text{[math]}$ ，当 $\text{[math]}$ 时，方程 $\text{[math]}$ 的两个根为 $\text{[math]}$ ，且满足下列条件：①该抛物线的“伴随矩形” $\text{[math]}$ 为正方形；② $\text{[math]}$ （其中 $\text{[math]}$ 表示矩形 $\text{[math]}$ 的面积）；③ $\text{[math]}$ 的最小值为 $\text{[math]}$ ．请求出满足条件的t值．
答案解析收藏纠错 + 选题

试卷信息