一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的)
-
-
-
-
4.
(2024七上·南关期末)
如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )
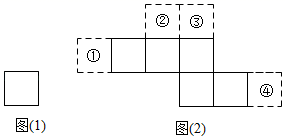
A . ①
B . ②
C . ③
D . ④
-
A . 6a2平方米
B . 7a2平方米
C . 8a2平方米
D . 12a2平方米
-
A . 圆形
B . 长方形
C . 三角形
D . 椭圆
-
A . 等腰三角形
B . 梯形
C . 正七边形
D . 五边形
-
8.
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
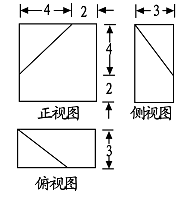
A . 108cm3
B . 100 cm3
C . 92cm3
D . 84cm3
二、填空题(每题3分,共15分)
-
9.
如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆 g.

-
10.
有一个正方体的六个面上分别标有数字1、2、3、4、5、6,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,那么a+b的值为 .

-
11.
一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有
种.

-
12.
如图是一个没有完全展开的正方体,若再剪开一条棱,则得到的平面展开图可能是下图中的
(填写字母)

-
13.
(2020七上·禅城期末)
如图,一个 5 ´ 5 ´ 5 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上 下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为
.

三、解答题(共7题;共61分)
-
14.
(2020七上·吉林期末)
小名准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,你能在图中的拼接图形上再接一个正方形画出阴影,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗?请在下面的图①和图②中画出两种不同的补充方法.
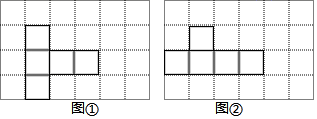
-
15.
有3个棱长分别是3cm,4cm,5cm的正方体组合成如图所示的图形.其露在外面的表面积是多少?(整个立体图形摆放在地上)

-
16.
如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
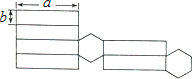
-
17.
如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
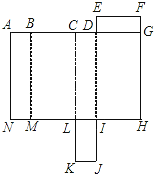
-
-
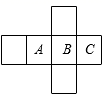
(1)
图1中的第个图形经过折叠不能围成无盖正方体纸盒(填序号).
-
(2)
小圣所在的综合实践小组把折叠成9个棱长都为

的无盖正方体纸盒摆成如图2所示的几何体.
①请计算出这个几何体的表面积;
②要保持从上面看到的平面图形不变,最多可以拿走小正方体的个数是 ▲ .
-
-
-
-
(3)
蛋糕的直径比盒子直径少3cm,高比盒子矮5cm,张琳打开盒子,沿着蛋糕底面的直径垂直切开,平均分成两部分,这时蛋糕的表面积增加多少平方厘米?
-
20.
如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.

问:
-
(1)
小立方体中三面红的有几块?两面红的呢?一面红的呢?没有红色的面呢?
-
-
 B .
B .  C .
C .  D .
D . 

 B .
B . 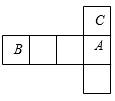 C .
C . 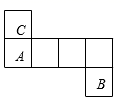 D .
D .