【培优版】新北师大版(2024)数学七上第三章整式及其加减 ...

更新时间：2024-07-17 浏览次数：37 类型：单元试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. (2024九下·武威模拟) 下列运算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
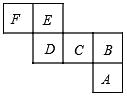
2. (2024七上·盘锦期末) 如果一个长方形内部能用一些正方形铺满，既不重叠，又无缝隙，就称为“优美长方形”，如图，“优美长方形” $\text{[math]}$ 的周长为78，则正方形 $\text{[math]}$ 的边长为（）

A . 6 B . 9 C . 12 D . 15

答案解析收藏纠错 + 选题
3. (2024七上·黔东南期末) 一个长方形的周长为 $\text{[math]}$ ，其中一边的长为 $\text{[math]}$ ，则另一边的长为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七上·仙居期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）．

A . 3 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七上·潮南期末) 已知一个多项式与 $\text{[math]}$ 的和为 $\text{[math]}$ ，则此多项式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七上·三台期末) 把六张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为acm ，宽为bcm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（　　）

A . 4bcm B . （3a+b）cm C . （2a+2b）cm D . （a+3b）cm

答案解析收藏纠错 + 选题
7. (2018七上·龙江期末) 如图，是一个正方体的平面展开图，且相对两个面表示的整式的和都相等，如果 $\text{[math]}$ $\text{[math]}$ ，则E所代表的整式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·邯郸经济技术开发期中) 在长方形ABCD内，将两张边长分别为a和 $\text{[math]}$ 的正方形纸片按图①，②两种方式放置（图①，②中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示.若 $\text{[math]}$ ，图①中阴影部分的面积表示为 $\text{[math]}$ ，图②中阴影部分的面积表示为 $\text{[math]}$ ， $\text{[math]}$ 的值与a，b，m，n四个字母中哪个字母的取值无关（）

A . 与a的取值无关 B . 与b的取值无关 C . 与m的取值无关 D . 与n的取值无关.

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. (2024七上·陕州期末) 已知数a、b、c在数轴上的位置如图所示，化简 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024七上·宁南期末) 若4x²y³+2ax²y³=4bx²y³ ，则3+a﹣2b=．

答案解析收藏纠错 + 选题
11. (2024七上·龙岗期末) 若 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023七上·潜江月考) 已知多项式 $\text{[math]}$ 为5次多项式，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024七上·怀集期末) 按一定规律排列的单项式： $\text{[math]}$ ，则第8个单项式为．

答案解析收藏纠错 + 选题

三、解答题（共7题；共61分）

14. (2024七上·陕州期末) 如图所示，池塘边有块长为20m，宽为10m的长方形土地，现在将其余三面留出宽都是xm的小路，中间余下的长方形部分做菜地，用含x的式子表示：
（1）菜地的长a=　　m，菜地的宽b=　　m；菜地的周长C=　　m；
（2）求当x=1m时，菜地的周长C．

答案解析收藏纠错 + 选题
15. (2023七上·东乡区期中) 阅读材料：“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．例如：已知 $\text{[math]}$ ，则代数式 $\text{[math]}$ ．请根据以上材料解答下列问题：
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为；
2. （2）当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值是5，求当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值；
3. （3）当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值为 $\text{[math]}$ ，求当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值（用含 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
16. (2023七上·前郭尔罗斯期中) 如图，在长方形中挖去两个三角形．
1. （1）用含a、b的式子表示图中阴影部分的面积S．
2. （2）当a＝8，b＝10时求图中阴影部分的面积．
答案解析收藏纠错 + 选题
17. (2023七上·吉林月考) 近年来，电商多选择在11月11日促销．今年的促销期间，某电商客服在为买家包装商品时用到长、宽、高分别为a厘米、b厘米、c厘米的箱子，并发现有如图所示的乙两种打包方式（打包带不计接头处的长）．回答下列问题：
1. （1）用含a，b， c的式子表示甲、乙两种打包方式所用的打包带的长度：
  甲需要厘米，乙需要厘米；
2. （2）当a=50厘米，b=40厘米，c=30厘米时，直接写出甲、乙两种打包方式所用的打包带的长度：甲需要厘米，乙需要厘米；
3. （3）当a>b>c时，两种打包方式中，哪种方式节省打包带？并说明你的理由．
答案解析收藏纠错 + 选题
18. (2023七上·长春期中) 复习整式的运算时，李老师在黑板上出了一道题，“已知A＝-x²＋4x，b＝2x²＋5x-4，当x＝-2时，求A＋B的值．”
1. （1）嘉嘉准确的计算出了正确答案-18，小明把“x＝-2”看成了“x＝2”，只是把x的值看错了，其余计算正确，通过计算说明小明的计算结果与嘉嘉的计算结果有什么关系．
2. （2）淇淇由于看错了B式中的一次项系数，比正确答案的值多了16，通过计算说明淇淇把B式中的一次项系数看成了什么数？
答案解析收藏纠错 + 选题
19. (2023七上·富川期中) 定义：若a+b＝2，则称a与b是关于M的平衡数．
1. （1） 5与是关于M的平衡数，1-x与是关于M的平衡数．（用含x的代数式表示）
2. （2）若a＝2x²-3（x²+x）+4，b＝2x-[3x-（4x+x²）-2]，判断a与b是否是关于M的平衡数，并说明理由．
答案解析收藏纠错 + 选题
20. (2024七上·北流期末) 我们定义：对于数对 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 称为“和积等数对”．如：因为 $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ ， $\text{[math]}$ 都是“和积等数对”．
1. （1）下列数对中，是“和积等数对”的是；（填序号）
  ① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ 是“和积等数对”，求x的值；
3. （3）若 $\text{[math]}$ 是“和积等数对”，求代数式 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题