广东省深圳市龙岗实验学校2024-2025学年九年级上学期开...

更新时间：2024-11-13 浏览次数：13 类型：开学考试

一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。

1. (2024九上·龙岗开学考) 芯片是半导体元件产品的统称，是一种将电路小型化的技术，常制造在半导体晶圆表面上 $\text{[math]}$ 下列关于芯片的图标中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·东莞期中) 下列方程是一元二次方程的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·龙岗开学考) 如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B沿地面向右滑行．在此滑动过程中，点P到点O的距离（）

A . 变小 B . 不变 C . 变大 D . 无法判断

答案解析收藏纠错 + 选题
4. (2024九上·沈阳月考) 如图，矩形ABCD的对角线AC，BD相交于点O， $\text{[math]}$ ， $\text{[math]}$ ，则矩形对角线的长为（）

A . 4 B . 8 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·龙岗开学考) 一元二次方程 $\text{[math]}$ 配方后可化为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九上·龙岗开学考) 实验室的一个容器内盛有 $\text{[math]}$ 克食盐水，其中含盐 $\text{[math]}$ 克 $\text{[math]}$ 如何处理能将该容器内食盐水含盐的百分比提高到原来的 $\text{[math]}$ 倍 $\text{[math]}$ 晓华根据这一情景中的数量关系列出方程 $\text{[math]}$ ，则未知数 $\text{[math]}$ 表示的意义是（）

A . 增加的水量 B . 蒸发掉的水量 C . 加入的食盐量 D . 减少的食盐量

答案解析收藏纠错 + 选题
7. (2024九上·龙岗开学考) 若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·龙岗开学考) 如图 $\text{[math]}$ ，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 的中点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 的速度运动到终点 $\text{[math]}$ 设点 $\text{[math]}$ 运动的时间为 $\text{[math]}$ 的面积为 $\text{[math]}$ ，图 $\text{[math]}$ 之间的函数关系图象，下列判断不正确的是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . 平行四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本题共5小题，每小题3分，共15分。

9. (2024九上·龙岗开学考) 已知方程2x²－mx＋3＝0的一个根是－1，则m的值是．

答案解析收藏纠错 + 选题
10. (2024九上·龙岗开学考) 如图， $\text{[math]}$ ， $\text{[math]}$ 两地被古城墙阻隔，为测量 $\text{[math]}$ ， $\text{[math]}$ 两地间的距离，先在城墙外地上取一个可以直接到达 $\text{[math]}$ ， $\text{[math]}$ 两地的点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，分别取 $\text{[math]}$ ， $\text{[math]}$ 的中点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ 的长为 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 两地间的距离为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九上·龙岗开学考) 门窗是中国古代木构架建筑上的重要组成部分．如图①所示是一款冰裂纹窗格，图②是窗格中的部分图案．其中 $\text{[math]}$ 是五边形 $\text{[math]}$ 的4个外角，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是°．

答案解析收藏纠错 + 选题
12. (2024九上·龙岗开学考) 已知关于x的不等式组 $\text{[math]}$ 只有3个整数解，则实数a的取值范围是．

答案解析收藏纠错 + 选题
13. (2024九上·龙岗开学考) 如图，正方形 $\text{[math]}$ 边长为 $\text{[math]}$ ，正方形 $\text{[math]}$ 边长为 $\text{[math]}$ ，连接 $\text{[math]}$ 和 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题：本题共7小题，共61分。解答应写出文字说明，证明过程或演算步骤。

14. (2024九上·龙岗开学考) 解方程：
1. （1） x²+2x-4＝0；
2. （2） 3x（2x+1）＝4x+2.
答案解析收藏纠错 + 选题
15. (2024九上·龙岗开学考) 先化简，再求值 $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. 如图：在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线交BC于点E（尺规作图的痕迹保留在图中了），连接EF．
1. （1）求证：四边形ABEF为菱形；
2. （2） AE，BF相交于点O，若BF=6，AB=5，求AE的长．
答案解析收藏纠错 + 选题
17. (2024九上·龙岗开学考) 阅读材料：
材料 $\text{[math]}$ ：若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个根为 $\text{[math]}$ ， $\text{[math]}$ ，则有 $\text{[math]}$ ， $\text{[math]}$ ．
材料 $\text{[math]}$ ：已知一元二次方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ 求 $\text{[math]}$ 的值．
解： $\text{[math]}$ 方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ，
$\text{[math]}$ ．
根据上述材料，结合你所学的知识，完成下列问题：
1. （1）材料理解：若一元二次方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）类比应用：已知一元二次方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值 $\text{[math]}$ ；
3. （3）思维拓展：已知实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
18. (2024九上·宣威期中) 社区利用一块矩形空地 $\text{[math]}$ 建了一个小型停车场，其布局如图所示．已知 $\text{[math]}$ ， $\text{[math]}$ ，阴影部分设计为停车位，要铺花砖，其余部分均为宽度为 $\text{[math]}$ 米的道路．已知铺花砖的面积为 $\text{[math]}$ ．
1. （1）求道路的宽是多少米？
2. （2）该停车场共有车位 $\text{[math]}$ 个，据调查分析，当每个车位的月租金为 $\text{[math]}$ 元时；可全部租出；若每个车位的月租金每上涨 $\text{[math]}$ 元，就会少租出 $\text{[math]}$ 个车位．当每个车位的月租金上涨多少元时，停车场的月租金收入为 $\text{[math]}$ 元
答案解析收藏纠错 + 选题

19. (2024九上·龙岗开学考) 阅读以下材料，并按要求完成相应的任务：

等腰梯形

在第六章，我们按照“定义一性质一判定”的路径研究了平行四边形 $\text{[math]}$ 生活中还有另一种特殊四边形一等腰梯形，我们可以类比平行四边形对其进行研究．

定义：只有一组对边平行的四边形叫做梯形，其中互相平行的两边叫做底，不平行的两边叫做腰 $\text{[math]}$ 两腰相等的梯形叫做等腰梯形．

如图 $\text{[math]}$ ，四边形 $\text{[math]}$ 是等腰梯形，其中 $\text{[math]}$ ， $\text{[math]}$ ．

性质：从整体对称性看，等腰梯形是轴对称图形：

从局部元素特征看，等腰梯形有如下性质：

性质 $\text{[math]}$ ：等腰梯形同一底上的两个角相等；性质 $\text{[math]}$ ： $\text{[math]}$

判定：与平行四边形类似，等腰梯形的性质与判定也具有互逆关系

判定 $\text{[math]}$ ： $\text{[math]}$ ．

任务：

（1）为证明等腰梯形的性质 $\text{[math]}$ ，小颖的思考如下 $\text{[math]}$ 请按她的思路选择一种方法写出证明过程．
已知：如图 $\text{[math]}$ ，四边形 $\text{[math]}$ 是等腰梯形， $\text{[math]}$ ， $\text{[math]}$ ．
求证： $\text{[math]}$ ， $\text{[math]}$ ．
证明：方法 $\text{[math]}$ ：过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线，交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ；
方法 $\text{[math]}$ ：过点 $\text{[math]}$ ， $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
（2）根据材料中的思路，小颖由等腰梯形的性质 $\text{[math]}$ 得到关于等腰梯形判定方法的猜想，请你补全该命题，并判断其真假： ▲ 的梯形是等腰梯形，该命题是 ▲ 命题．

答案解析收藏纠错 + 选题

20. (2024九上·龙岗开学考) 【材料背景】
如图 $\text{[math]}$ ，在 $\text{[math]}$ 中，以边 $\text{[math]}$ 为底边向外作等腰 $\text{[math]}$ ，其中 $\text{[math]}$ ，且 $\text{[math]}$ ，那么点 $\text{[math]}$ 就被称为边 $\text{[math]}$ 的“外展等直点”．
【建构与探究】
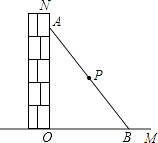
如图 $\text{[math]}$ ，正方形网格是由边长为“ $\text{[math]}$ ”的正方形组成，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在格点上， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点．
1. （1）连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，请分别作边 $\text{[math]}$ 、 $\text{[math]}$ 的“外展等直点” $\text{[math]}$ 和 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ ，则 $\text{[math]}$ 的形状为 ▲ ；
2. （2）如图 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 在格点上，请在线段 $\text{[math]}$ 上的格点中任取一点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，分别作 $\text{[math]}$ 的边 $\text{[math]}$ 和边 $\text{[math]}$ 的“外展等直点” $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ ，请判断 $\text{[math]}$ 的形状，并说明理由．
3. （3）【应用与拓展】
  如图 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 为平面内某三角形两条边的“外展等直点”，已知 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出该三角形第三条边的中点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题