安徽省滁州市全椒县2017年中考数学三模试卷

更新时间：2017-12-14 浏览次数：471 类型：中考模拟

一、选择题

1. (2017·全椒模拟) 实数﹣ $\text{[math]}$ 的绝对值是（）

A . 5 B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·全椒模拟) 下列计算正确的是（）

A . $\text{[math]}$ × $\text{[math]}$ = $\text{[math]}$ B . x⁸÷x²=x⁴ C . （2a）³=6a³ D . 3a⁵•2a³=6a⁶

答案解析收藏纠错 + 选题
3. (2017·全椒模拟) 因式分解x²y﹣4y的结果是（）

A . y（x²﹣4） B . y（x﹣2）² C . y（x+4）（x﹣4） D . y（x+2）（x﹣2）

答案解析收藏纠错 + 选题
4. (2019·河南模拟) 将一根圆柱形的空心钢管任意放置，它的主视图不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019九上·梅县期中) 某校九年级共有1、2、3、4四个班，现从这四个班中随机抽取两个班进行一场篮球比赛，则恰好抽到1班和2班的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·昆明模拟) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021八下·禹城期中) 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）

A . 78° B . 75° C . 60° D . 45°

答案解析收藏纠错 + 选题
8. 如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（）

A . 44° B . 66° C . 88° D . 92°

答案解析收藏纠错 + 选题
9. (2017·全椒模拟) 如图，AC，BD相交于点O，且OA=OC=4，OB=OD=6，P是线段BD上一动点，过点P作EF∥AC，与四边形的两条边分别交于点E，F，设BP=x，EF=y，则下列能表示y与x之间函数关系的图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2017·全椒模拟) 如图，菱形ABCD的边长为2，∠ABC=60°，E是AD的中点，点P是对角线BD上的动点，当AP+PE的值最小时，PC的长是（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2017·全椒模拟) 我国计划在2020年左右发射火星探测卫星．据科学研究，火星距离地球的最近距离约为5500万千米，这个数据用科学记数法可表示为千米．

答案解析收藏纠错 + 选题
12. (2017·全椒模拟) 若x²﹣3y﹣5=0，则6y﹣2x²﹣6=．

答案解析收藏纠错 + 选题
13. (2017·全椒模拟) 如图，在矩形ABCD中，AD=6，AB=4，点E，G，H，F分别在AB，BC，CD，AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连接PE，PF，PG，PH，则△PEF和△PGH的面积和等于．

答案解析收藏纠错 + 选题
14. (2017·全椒模拟) 如图，边长为2的正方形ABCD内接于⊙O，点E是 $\text{[math]}$ 上一点（不与A、B重合），点F是 $\text{[math]}$ 上一点，连接OE，OF，分别与AB，BC交于点G，H，有下列结论：
① $\text{[math]}$ = $\text{[math]}$ ；
②△OGH是等腰三角形；
③四边形OGBH的面积随着点E位置的变化而变化；
④若BG=1﹣ $\text{[math]}$ ，则BG，GE， $\text{[math]}$ 围成的面积是 $\text{[math]}$ + $\text{[math]}$ ．
其中正确的是（把所有正确结论的序号都填上）

答案解析收藏纠错 + 选题

三、综合题

15. (2017·全椒模拟) 计算：（ $\text{[math]}$ +1）⁰﹣2^﹣¹+ $\text{[math]}$ ﹣6sin60°．

答案解析收藏纠错 + 选题
16. (2017·全椒模拟) 观察下列等式：
① $\text{[math]}$ + $\text{[math]}$ ﹣ $\text{[math]}$ = $\text{[math]}$ ；
② $\text{[math]}$ + $\text{[math]}$ ﹣ $\text{[math]}$ = $\text{[math]}$ ；
③ $\text{[math]}$ + $\text{[math]}$ ﹣ $\text{[math]}$ = $\text{[math]}$ ；
④ $\text{[math]}$ + $\text{[math]}$ ﹣ $\text{[math]}$ = $\text{[math]}$ ；
…
1. （1）请按以上规律写出第⑤个等式：；
2. （2）猜想并写出第n个等式：；
3. （3）请证明猜想的正确性．
答案解析收藏纠错 + 选题
17. (2017·全椒模拟) 如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC在平面直角坐标系中的位置如图所示．

①画出与△ABC关于y轴对称的△A₁B₁C₁ ，求点C₁的坐标。

②以原点O为位似中心，在第四象限画一个△A₂B₂C₂ ，使它与△ABC位似，并且△A₂B₂C₂与△ABC的相似比为2：1．

答案解析收藏纠错 + 选题
18. (2017·全椒模拟) 如图，我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋，立即通知在B处的另一艘军舰一起向其包抄，此时B在A的南偏西30°方向，我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向，已知A，B之间的距离是30海里，求此刻我两艘军舰所在地A，B与C的距离．（结果保留根号）

答案解析收藏纠错 + 选题
19. (2017·全椒模拟) 某校为了美化校园计划购买茶花、桂花两种树苗共600株，茶花树苗每株35元，桂花树苗每株40元．相关资料表明：茶花、桂花树苗的成活率分别为80%，90%．
1. （1）若购买这两种树苗共用去22000元，则茶花、桂花树苗各购买多少株？
2. （2）若要使这批树苗的总成活率不低于85%，则茶花树苗至多购买多少株？
3. （3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低，并求出最低费用．
答案解析收藏纠错 + 选题
20. (2017·全椒模拟) 某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣，利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查．
造成医患关系紧张的原因（单选）
A．药价高
B．检测项目太多且收费太高
C．住院报销比例低
D．医疗费与个人收入不相称
E．其他
根据调查结果绘制出了如下两幅尚不完整的统计图．
根据以上信息解答下列问题：
1. （1）这次接受调查的总人数为人；
2. （2）在扇形统计图中，“A”所在扇形的圆心角的度数为；
3. （3）补全条形统计图；
4. （4）若该市有1000万人，请你估计选D的总人数．
答案解析收藏纠错 + 选题
21. (2017·全椒模拟) 如图，直线AB经过x轴上的点M，与反比例函数y= $\text{[math]}$ （x＞0）的图象相交于点A（1，8）和B（m，n），其中m＞1，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P．
1. （1）求k的值；
2. （2）若AB=2BM，求△ABD的面积；
3. （3）若四边形ABCD为菱形，求直线AB的函数解析式．
答案解析收藏纠错 + 选题
22. (2017·全椒模拟) 如图
1. （1）问题：如图①，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．
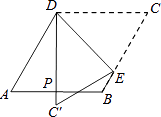
  求证：AD•BC=AP•BP．
2. （2）探究：如图②，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ，上述结论是否依然成立？说明理由．
3. （3）应用：请利用（1）（2）获得的经验解决问题：
  如图③，在△ABD中，AB=6，AD=BD=5，点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A，设点P的运动时间为t秒，当以D为圆心，以DC为半径的圆与AB相切时，求t的值．
答案解析收藏纠错 + 选题
23. (2017·全椒模拟) 已知抛物线y=ax²+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．
1. （1）当h=1，k=2时，求抛物线的解析式；
2. （2）若抛物线y=tx²（t≠0）也经过点A，过a与t之间的关系式；
3. （3）在（2）的条件下，已知a=﹣ $\text{[math]}$ ，直线l：y= $\text{[math]}$ x﹣1与抛物线y=tx²﹣ $\text{[math]}$ x﹣7交于点B，C，与x轴，y轴交于点D，E，点M在抛物线y=tx²﹣ $\text{[math]}$ x﹣7上，且点M的横坐标为m（0＜m＜6）．MF∥y轴交于直线l于点F，点N在直线l上，且四边形MNFQ为矩形（如图），若矩形MNFQ的周长为P，求P的最大值．
答案解析收藏纠错 + 选题