一、选择题:本题共8小题,每小题4分,共32分.在每小题给出的选项中,只有一项是符合题目要求的.
-
A . 3.14
B . - C . 0.57
D . π
C . 0.57
D . π
-
A . 2
B . -2
C . ±2
D . 16
-
-
A . 1、2、3
B . 2、3、4
C . 3、4、5
D . 4、5、6
-
-
A . x≥3
B . x≥﹣3
C . x≥3且x≠0
D . x≥﹣3且x≠0
-
-
8.
(2024七下·长沙期末)
明代《算法统宗》有一首饮酒数学诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醇酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人:薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒
x瓶,薄酒
y瓶.根据题意,可列方程组为( )
二、填空题:本题共10小题,每小题4分,共40分.
-
-
-
-
12.
(2024八上·金牛期中)
一个长方体形盒子的长、宽、高分别为2cm、2cm、3cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,则这只蚂蚁要爬行的最短距离是
.

-
-
14.
(2024八上·金牛期中)
如图,数轴上的点

表示的数是

, 点

表示的数是1,

于点

, 且

, 以点

为圆心,

为半径画弧交数轴于点

, 则点

表示的数为
.

-
-
16.
(2024八上·金牛期中)
如图,在等腰直角三角形

中,

, 点

,

分别为

,

上的动点,且

,

. 当

的值最小时,
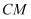
的长为
.

-
17.
(2024八上·金牛期中)
如图,在平面直角坐标系中,

、

、

、…、

均为等腰直角三角形,且

, 点

、

、

、…、

和点

、

、

、…、

分别在正比例函数

和

的图象上,且点

、

、

、…、

的横坐标分别为1,2,3…n,线段

、

、

、…、

均与

轴平行,按照图中所反映的规律,则

的顶点

的坐标是
;线段

的长是
.(其中

为正整数)

三、计算题:本大题共1小题,共10分.
-
18.
(2024八上·金牛期中)
(1)如图①,

是等边

内一点,

,

,

, 将线段

绕点

逆时针旋转

得到线段

, 连结线段

,

, 试判断

的形状.

(2)点 是以
是以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 内一点,且
内一点,且 ,
,  ,
,  .
.
①求 的度数;
的度数;
②求 的面积.
的面积.
四、解答题:本题共7小题,共68分.解答应写出文字说明,证明过程或演算步骤.
-
-
(1)

;
-
(2)

.
-
-
(1)

;
-
(2)

.
-
-
(1)

;
-
(2)

.
-
-
-
(2)
求出

的面积;
-
-
-
(1)
求

的值.
-
(2)
若

的小数部分为

,

的整数部分为

, 求

的平方根.
-
-
(1)
填空:

________,

________;
-
(2)
如果在第三象限内有一点

, 在

轴负半轴上有一点

, 使得

的面积与

的面积相等,求出

点的坐标;
-
(3)
在(2)问的条件下,在

轴上存在

点,使

为等腰三角形,求出点

的坐标.
-
25.
(2024九下·长春模拟)
在

中,

, 点D是平面内一点(不与点A,B,C重合),连接

, 连接

. 将

沿直线

翻折,得到

, 连接

.

-
(1)
如图1,点D在

内部,

交

于点E,点F是

上一点,且

, 连接

.
①求证: ;
;
②若 ,
,  , 求点G到直线
, 求点G到直线 的距离.
的距离.
-
(2)
如图2,点D在

的内部,试探究

之间的数量关系并说明理由.
 B .
B .  C .
C .  D .
D . 



是以
为斜边的等腰直角三角形
内一点,且
,
,
.
的度数;
的面积.
;
,
, 求点G到直线
的距离.