山东省青岛市2017年中考数学模拟试卷

更新时间：2024-07-12 浏览次数：679 类型：中考模拟

一、选择题

1. (2017·青岛模拟) 下列命题中错误的是（）

A . ﹣2017的绝对值是2017 B . 3的平方根是 $\text{[math]}$ C . ﹣ $\text{[math]}$ 的倒数是﹣ $\text{[math]}$ D . 0的相反数是0

答案解析收藏纠错 + 选题
2. (2017·青岛模拟) 如图所示的三种视图所对应的几何体是（箭头为主视图方向）（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2017·青岛模拟) 2016年11月17日，我国在酒泉卫星发射中心使用长征二号FY11运载火箭成功将神舟十一号载人飞船送入太空，此次神舟十一号顺利升空是中国航天的又一次重大胜利．神舟十一号和天宫二号对接时的轨道高度是393千米，比过去高了50千米.393千米可以用科学记数法表示为（）米．

A . 3.93×10⁵ B . 3.93×10⁶ C . 3.93×10⁴ D . 0.393×10⁶

答案解析收藏纠错 + 选题
4. (2017·青岛模拟) 下列四个图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017·青岛模拟) 某工厂甲、乙两名工人参加操作技能培训．他们在培训期间参加的8次测试成绩记录如下表：
甲
73
82
70
85
80
70
75
65
乙
85
72
78
71
83
69
74
68
则下列说法错误的是（）

A . 甲、乙的平均成绩都是75 B . 甲成绩的众数是70 C . 乙成绩的中位数是73 D . 若从中选派一人参加操作技能比赛，从成绩稳定性考虑，应选甲

答案解析收藏纠错 + 选题
6. 如图，扇形AOB的半径为2，∠AOB=90°，以AB为直径画半圆．则图中阴影部分（即半圆在扇形AOB外部分）的面积为（）

A . 4 B . 3π+2 C . 2 D . π﹣2

答案解析收藏纠错 + 选题
7. (2017·青岛模拟) 如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2 $\text{[math]}$ ，∠DCF=30°，则EF的长为（）

A . 4 B . 6 C . $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2017·青岛模拟) 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣5，0），对称轴为直线x=﹣2，给出四个结论：①b²＞4ac；②4a+b=0；③函数图象与x轴的另一个交点为（2，0）；④若点（﹣4，y₁）、（﹣1，y₂）为函数图象上的两点，则y₁＜y₂ ．其中正确结论是（）

A . ②④ B . ①④ C . ①③ D . ②③

答案解析收藏纠错 + 选题

二、填空题

9. (2021八下·崂山开学考) 计算： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
10. (2017·青岛模拟) 如图，在平面直角坐标系中，线段AB的两个端点是A（﹣5，1），B（﹣2，3），平移线段AB得到线段A₁B₁ ，若点A的对应点A₁的坐标为（1，2），则点B的对应点B₁的坐标为．

答案解析收藏纠错 + 选题
11. (2017·青岛模拟) 如图，点A、B、C、D都在⊙O上，∠ABC=90°，AD=2，CD=1，则⊙O的直径的长是．

答案解析收藏纠错 + 选题
12. (2017·青岛模拟)
如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B围成的正方体上的距离是

答案解析收藏纠错 + 选题
13. (2017·青岛模拟) 某文化用品商店计划同时购进一批A、B两种型号的计算器，若购进A型计算器10只和B型计算器8只，共需要资金880元；若购进A型计算器2只和B型计算器5只，共需要资金380元．则A型号的计算器的每只进价为元．

答案解析收藏纠错 + 选题
14. (2017·青岛模拟) 有一组多项式：a﹣b² ， a³+b⁴ ， a⁵﹣b⁶ ， a⁷+b⁸ ， …，请观察它们的构成规律，用你发现的规律写出第n个多项式为．

答案解析收藏纠错 + 选题

三、作图题

15. (2017·青岛模拟) 如图，工人师傅要利用一块形状为直角三角形（∠C为直角）的铁皮加工一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．请作出这个正方形零件在AB边上的顶点M．

答案解析收藏纠错 + 选题

四、解答题

16. (2017·青岛模拟) 计算题
1. （1）解不等式组： $\text{[math]}$ ．
2. （2）化简：（x﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2017·青岛模拟) 青岛是全车著名的海滨旅游城市，有丰富的旅游产品．某校九年级（1）班的同学就部分旅游产品的喜爱情况对游客随机调查，要求游客在列举的旅游产品中选出喜爱的产品，且只能选一项．以下是同学们根据游客选择整理的不完整的统计图（图①为旅游产品喜爱情况条形统计图，图②为旅游产品喜爱情况扇形统计图）：
根据以上信息完成下列问题：
1. （1）随机调查的游客有多少人；在扇形统计图中，A部分所占的圆心角是多少度．
2. （2）请将条形统计图①补充完整．
3. （3）请根据调查结果估计在3000名游客中喜爱大泽山葡萄的约有多少人．
答案解析收藏纠错 + 选题
18. (2017·青岛模拟) 小明与小亮玩游戏，如图，两组相同的卡片，每组三张，第一组卡片正面分别标有数字1，3，5；第二组卡片正面分别标有数字2，4，6．他们将卡片背面朝上，分组充分洗匀后，从每组卡片中各摸出一张，称为一次游戏．当摸出的两张卡片的正面数字之积小于10，则小明获胜；当摸出的两张卡片的正面数字之积超过10，则小亮获胜．你认为这个游戏规则对双方公平吗？请说明理由．

答案解析收藏纠错 + 选题
19. (2017·青岛模拟) 如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截．红方行驶26千米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西37°方向前进，刚好在D处成功拦截蓝方．求拦截点D处到公路的距离AD．
（参考数据：sin67°≈ $\text{[math]}$ ，cos67°≈ $\text{[math]}$ ，tan67°≈ $\text{[math]}$ ，sin37°≈ $\text{[math]}$ ，cos37°≈ $\text{[math]}$ ，tan37°≈ $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2017·青岛模拟) 某工厂设计了一款产品，成本价为每件10元．投放市场进行试销，得到如下数据：
售价x（元/件）
…
30
40
50
60
…
日销售量y（件）
…
50
40
30
20
…
1. （1）若日销售量y（件）是售价x（元/件）的一次函数，求这个一次函数解析式．
2. （2）设这个工厂试销该产品每天获得的利润为w（元），当售价定为每件多少元时，工厂每天获得的利润最大？最大利润是多少元？（每天利润=每天销售总收入﹣每天销售总成本）
答案解析收藏纠错 + 选题
21. (2017·青岛模拟) 如图，已知四边形BCDE为平行四边形，点A在BE的延长线上且AE=EB．连接EC，AC，AD．
1. （1）求证：△AED≌△EBC．
2. （2）若∠ACB=90°，则四边形AECD是什么特殊四边形？请说明理由．
答案解析收藏纠错 + 选题
22. (2017·青岛模拟) 改革开放以来，国家经济实力和国民生活水平不断提高，但经济发展的同时对环境产生了较大的污染，环境治理已刻不容缓．某市为加快环境治理，引进新的垃圾处理设备，计划对该市2017年第一季度沿河收集的6000吨垃圾进行集中处理．
1. （1）写出处理完这批垃圾所用时间y（天）关于日均垃圾处理量x（吨）的函数关系式．
2. （2）该市垃圾实际处理过程中由于提高效能，日均垃圾处理量比原计划多20%，结果比原计划少用5天处理完全部垃圾，求原计划日均垃圾处理量为多少吨．
答案解析收藏纠错 + 选题
23. (2017·青岛模拟) 问题提出：如何将一个长为17，宽为1的长方形经过剪一剪，拼一拼，形成一个正方形．（下列所有图中每个小方格的边长都为1，剪拼过程中材料均无剩余）
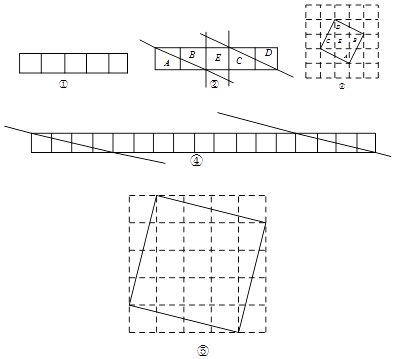
问题探究：我们从长为5，宽为1的长方形入手．
1. （1）如图①是一个长为5，宽为1的长方形．把这个长方形剪一剪、拼一拼后形成正方形，则正方形的面积应为，设正方形的边长为a，则a=．
2. （2）我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式，比如 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．类比此，可以将（1）中的a表示成a=．
3. （3） $\text{[math]}$ = $\text{[math]}$ 的几何意义可以理解为：以长度2和3为直角边的直角三角形的斜边长为 $\text{[math]}$ ；类比此，（2）中的a可以理解为以长度和为直角边的直角三角形斜边的长．
4. （4）剪一剪：由（3）可画出如图②的分割线，把长方形分成A、B、C、D、E五部分．
5. （5）拼一拼：把图②中五部分拼接得到如图③的正方形．
  问题解决：仿照上面的探究方法请把图④中长为17，宽为1的长方形剪一剪，在图⑤中画出拼成的正方形．（说明：图④的分割过程不作评分要求，只对图⑤中画出的最终结果评分）
答案解析收藏纠错 + 选题
24. (2017·青岛模拟) 如图，在Rt△ABC中，∠C=90°，AB=10cm，AC=8cm．点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s．当一个动点到达终点时，另一个动点也随之停止运动．设运动时间为t（s）．
1. （1）当t为何值时，△APC为等腰三角形．
2. （2）当点Q在线段BC上运动时，△PBQ的面积为S（cm²），写出S与t之间的函数关系．
3. （3）当点Q在线段BC上运动时，是否存在某一时刻t，使S_△_PBQ：S_四边形_APQC=5：3？若存在，求出t值；若不存在，说明理由．
4. （4）在运动过程中，是否存在某一时刻t，使BQ平分∠ABC？若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题