河北省邢台市2016-2017学年高二下学期理数期末考试试卷

更新时间：2018-02-07 浏览次数：304 类型：期末考试

一、选择题

1. (2017高二下·邢台期末) 已知复数z满足zi⁵=1+2i，则 $\text{[math]}$ 在复平面内对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
2. (2017高二下·邢台期末) 两个变量y与x的回归模型中，分别选择了4个不同模型，它们对应的R²=1﹣ $\text{[math]}$ 的值如下，其中拟合效果最好的模型是（）

A . 模型1对应的R²=0.48 B . 模型3对应的R²=0.15 C . 模型2对应的R²=0.96 D . 模型4对应的R²=0.30

答案解析收藏纠错 + 选题
3. (2017高二下·邢台期末) 用数学归纳法证明“凸n变形对角线的条数f（n）= $\text{[math]}$ ”时，第一步应验证（）

A . n=1成立 B . n=2成立 C . n=3成立 D . n=4成立

答案解析收藏纠错 + 选题
4. (2017高二下·邢台期末) 下列曲线中，在x=1处切线的倾斜角为 $\text{[math]}$ 的是（）

A . y=x²﹣ $\text{[math]}$ B . y=xlnx C . y=sin（πx） D . y=x³﹣2x²

答案解析收藏纠错 + 选题
5. (2017高二下·邢台期末) 已知随机变量X服从正态分布N（100，4），若P（102＜X＜m）=0.1359，则m等于[驸：P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544]（）

A . 103 B . 104 C . 105 D . 106

答案解析收藏纠错 + 选题
6. (2017高二下·邢台期末) 把3名新生分到甲、乙、丙、丁四个班，每个班至多分配1名且甲班必须分配1名，则不同的分配方法有（）

A . 12种 B . 15种 C . 18种 D . 20种

答案解析收藏纠错 + 选题
7. (2017高二下·邢台期末) 给出下面三个类比结论：
①向量 $\text{[math]}$ ，有| $\text{[math]}$ |²= $\text{[math]}$ ²；类比复数z，有|z|²=z²
②实数a，b有（a+b）²=a²+2ab+b²；类比向量 $\text{[math]}$ ， $\text{[math]}$ ，有（ $\text{[math]}$ ）²= $\text{[math]}$ ² $\text{[math]}$ ²
③实数a，b有a²+b²=0，则a=b=0；类比复数z₁ ， z₂ ，有z₁²+z₂²=0，则z₁=z₂=0
其中类比结论正确的命题个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
8. (2017高二下·邢台期末) $\text{[math]}$ 展开式中任取一项，则所取项是有理项的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2017高二下·邢台期末) 袋中有6个黄色、4个白色的乒乓球，做不放回抽样，每次任取1个球，取2次，则关于事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率说法正确的是（）

A . 事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下，第二次恰好取得黄球”的概率都等于 $\text{[math]}$ B . 事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下，第二次恰好取得黄球”的概率都等于 $\text{[math]}$ C . 事件“直到第二次才取到黄色球”的概率等于 $\text{[math]}$ ，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于 $\text{[math]}$ D . 事件“直到第二次才取到黄色球”的概率等于 $\text{[math]}$ ，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2017高二下·邢台期末) 已知f（x）= $\text{[math]}$ ，设f₁（x）=f（x），f_n（x）=f_n_﹣1[f_n_﹣1（x）]（n＞1，n∈N*），若f_m（x）= $\text{[math]}$ （m∈N*），则m等于（）

A . 9 B . 10 C . 11 D . 126

答案解析收藏纠错 + 选题
11. (2017高二下·邢台期末) 3男3女共6名同学从左至右排成一排合影，要求左端排男同学，右端排女同学，且女同学至多有2人排在一起，则不同的排法种数为（）

A . 144 B . 160 C . 180 D . 240

答案解析收藏纠错 + 选题
12. (2017高二下·邢台期末) 已知函数f（x）=﹣ $\text{[math]}$ （a＞0）在区间[0，1]上有极值，且函数f（x）在区间[0，1]上的最小值不小于﹣ $\text{[math]}$ ，则a的取值范围是（）

A . （2，5] B . （2，+∞） C . （1，4} D . [5，+∞）

答案解析收藏纠错 + 选题

二、填空题

13. (2017高二下·邢台期末) 若（2x²﹣3）ⁿ展开式中第3项的二项式系数为15，则n=．

答案解析收藏纠错 + 选题
14. (2017高二下·邢台期末) 曲线f（x）=sin（ $\text{[math]}$ ﹣x）与直线x=﹣ $\text{[math]}$ ，x= $\text{[math]}$ ，y=0所围成的平面图形的面积为．

答案解析收藏纠错 + 选题
15. (2017高二下·邢台期末) 已知复数z=（2a+i）（1﹣bi）的实部为2，其中a，b为正实数，则4^a+（ $\text{[math]}$ ）^1﹣b的最小值为．

答案解析收藏纠错 + 选题
16. (2017高二下·邢台期末) 某校组织“中国诗词”竞赛，在“风险答题”的环节中，共为选手准备了A、B、C三类不同的题目，选手每答对一个A类、B类或C类的题目，将分别得到300分、200分、100分，但如果答错，则相应要扣去300分、200分、100分，根据平时训练经验，选手甲答对A类、B类或C类题目的概率分别为0.6、0.75、0.85，若腰每一次答题的均分更大一些，则选手甲应选择的题目类型应为（填A、B或C）

答案解析收藏纠错 + 选题

三、解答题

17. (2017高二下·邢台期末) 为了调查喜欢旅游是否与性别有关，调查人员就“是否喜欢旅游”这个问题，在火车站分别随机调研了50名女性和50名男性，根据调研结果得到如图所示的等高条形图
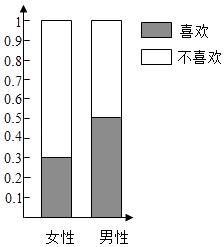
（Ⅰ）完成下列2×2列联表：

喜欢旅游
不喜欢旅游
合计
女性

男性

合计

（II）能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
附：
P（K²≥k₀）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k₀
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：K²= $\text{[math]}$ ，其中n=a+b+c+d）

答案解析收藏纠错 + 选题
18. (2017高二下·邢台期末) 国内某汽车品牌一个月内被消费者投诉的次数用X表示，据统计，随机变量X的概率分布如下：
X
0
1
2
3
P
0.1
0.3
2a
a
1. （1）求a的值；
2. （2）假设一月份与二月份被消费者投诉的次数互不影响，求该汽车品牌在这两个月内共被消费者投诉2次的概率．
答案解析收藏纠错 + 选题
19. (2017高二下·邢台期末) 已知函数f（x）=x³+ax²+bx+a²（a、b∈R）
1. （1）若函数f（x）在x=1处有极值为10，求b的值；
2. （2）若a=﹣4，f（x）在x∈[0，2]上单调递增，求b的最小值．
答案解析收藏纠错 + 选题
20. (2017高二下·邢台期末) 已知a＞0，b＞0．
1. （1）求证： $\text{[math]}$ + $\text{[math]}$ ≥ $\text{[math]}$ ；
2. （2）若c＞0，求证：在a﹣b﹣c，b﹣a﹣c，c﹣a﹣b中至少有两个负数．
答案解析收藏纠错 + 选题
21. (2017高二下·邢台期末) 中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康，某校为了解甲、乙两班每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取6名同学进步调查，将他们最近一周自我熬夜学习的总时长作为样本数据，绘制成茎叶图如图所示（图中的茎表示十位数字，叶表示个位数字）．如果学生平均每周
自我熬夜学习的总时长超过21小时，则称为“过度熬夜”．
（Ⅰ）请根据样本数据，分别估计甲，乙两班的学生平均每周自我熬夜学习时长的平均值；
（Ⅱ）从甲班的样本数据中有放回地抽取2个数据，求恰有1个数据为“过度熬夜”的概率；
（Ⅲ）从甲班、乙班的样本中各随机抽取2名学生的数据，记“过度熬夜”的学生人数为X，写出X的分布列和数学期望E（X）．

答案解析收藏纠错 + 选题
22. (2017高二下·邢台期末) 已知函数f（x）=（2x+b）e^x ， F（x）=bx﹣lnx，b∈R．
1. （1）若b＜0，且存在区间M，使f（x）和F（x）在区间M上具有相同的单调性，求b的取值范围；
2. （2）若F（x+1）＞b对任意x∈（0，+∞）恒成立，求b的取值范围．
答案解析收藏纠错 + 选题