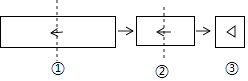
 B .
B .  C .
C .  D .
D . 

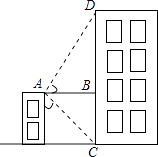


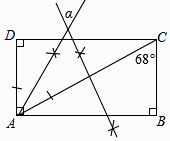
邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
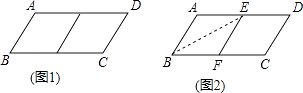
邻边长分别为3和5的平行四边形是阶准菱形;已知▱ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出▱ABCD是阶准菱形.
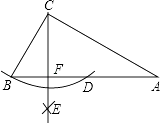
小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
