2018年中考数学专题高分攻略6讲专题五数学应用型问题

更新时间：2018-05-11 浏览次数：1178 类型：二轮复习

一、单选题

1. (2022九下·南宁模拟)
如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m² ．若设道路的宽为xm，则下面所列方程正确的是（）

A . （32﹣2x）（20﹣x）=570 B . 32x+2×20x=32×20﹣570 C . （32﹣x）（20﹣x）=32×20﹣570 D . 32x+2×20x﹣2x²=570

答案解析收藏纠错 + 选题

二、填空题

2. (2017·烟台) 运行程序如图所示，从“输入实数x”到“结果是否＜18”为一次程序操作，
若输入x后程序操作仅进行了一次就停止，则x的取值范围是．

答案解析收藏纠错 + 选题
3. (2017·温州)
小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为cm．

答案解析收藏纠错 + 选题

三、解答题

4. (2017·青海) 如图，建设“幸福西宁”，打造“绿色发展样板城市”．美丽的湟水河宛如一条玉带穿城而过，已形成“水清、流畅、岸绿、景美”的生态环境新格局．在数学课外实践活动中，小亮在海湖新区自行车绿道北段AC上的A，B两点分别对南岸的体育中心D进行测量，分别测得∠DAC=30°，∠DBC=60°，AB=200米，求体育中心D到湟水河北岸AC的距离约为多少米（精确到1米， $\text{[math]}$ ≈1.732）？

答案解析收藏纠错 + 选题
5. (2017·新疆)
如图，甲、乙为两座建筑物，它们之间的水平距离BC为30m，在A点测得D点的仰角∠EAD为45°，在B点测得D点的仰角∠CBD为60°，求这两座建筑物的高度（结果保留根号）

答案解析收藏纠错 + 选题
6. (2020·定远模拟) 我市某校组织爱心捐书活动，准备将一批捐赠的书打包寄往贫困地区，其中每包书的数目相等．第一次他们领来这批书的 $\text{[math]}$ ，结果打了16个包还多40本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了9个包，那么这批书共有多少本？

答案解析收藏纠错 + 选题
7. (2017·湖州) 湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了 $\text{[math]}$ $\text{[math]}$ 淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养 $\text{[math]}$ 天的总成本为 $\text{[math]}$ 万元；放养 $\text{[math]}$ 天的总成本为 $\text{[math]}$ 万元（总成本=放养总费用+收购成本）．
1. （1）设每天的放养费用是 $\text{[math]}$ 万元，收购成本为 $\text{[math]}$ 万元，求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
2. （2）
  设这批淡水鱼放养 $\text{[math]}$ 天后的质量为 $\text{[math]}$ （ $\text{[math]}$ ），销售单价为 $\text{[math]}$ 元/ $\text{[math]}$ ．根据以往经验可知： $\text{[math]}$ 与 $\text{[math]}$ 的函数关系为 $\text{[math]}$ ； $\text{[math]}$ 与 $\text{[math]}$ 的函数关系如图所示．
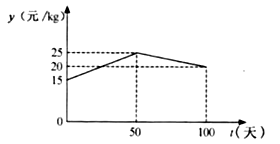
  ①分别求出当 $\text{[math]}$ 和 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
  ②设将这批淡水鱼放养 $\text{[math]}$ 天后一次性出售所得利润为 $\text{[math]}$ 元，求当 $\text{[math]}$ 为何值时， $\text{[math]}$ 最大？并求出最大值．（利润=销售总额-总成本）
答案解析收藏纠错 + 选题
8. (2020·乌兰浩特模拟) 美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图，测得∠DAC=45°，∠DBC=65°．若AB=132米，求观景亭D到南滨河路AC的距离约为多少米？（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

答案解析收藏纠错 + 选题

四、综合题

9. (2017·重庆) 某地大力发展经济作物，其中果树种植已初具规模，今年受气候、雨水等因素的影响，樱桃较去年有小幅度的减产，而枇杷有所增产．
1. （1）该地某果农今年收获樱桃和枇杷共400千克，其中枇杷的产量不超过樱桃产量的7倍，求该果农今年收获樱桃至少多少千克？
2. （2）该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售，该果农去年樱桃的市场销售量为100千克，销售均价为30元/千克，今年樱桃的市场销售量比去年减少了m%，销售均价与去年相同，该果农去年枇杷的市场销售量为200千克，销售均价为20元/千克，今年枇杷的市场销售量比去年增加了2m%，但销售均价比去年减少了m%，该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额与他去年樱桃和枇杷的市场销售总金额相同，求m的值．
答案解析收藏纠错 + 选题
10. (2021·固始模拟) 某新建成学校举行美化绿化校园活动，九年级计划购买A，B两种花木共100棵绿化操场，其中A花木每棵50元，B花木每棵100元．
1. （1）若购进A，B两种花木刚好用去8000元，则购买了A，B两种花木各多少棵？
2. （2）如果购买B花木的数量不少于A花木的数量，请设计一种购买方案使所需总费用最低，并求出该购买方案所需总费用．
答案解析收藏纠错 + 选题
11. (2020八上·遵化期末) 为了尽快实施“脱贫致富奔小康”宏伟意图，某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗，已知一棵苹果树苗比一棵梨树苗贵2元，购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元．
1. （1）若两种树苗购买的棵数一样多，求梨树苗的单价；
2. （2）若两种树苗共购买1100棵，且购买两种树苗的总费用不超过6000元，根据（1）中两种树苗的单价，求梨树苗至少购买多少棵．
答案解析收藏纠错 + 选题
12. (2017·百色) 某校九年级10个班级师生举行毕业文艺汇演，每班2个节目，有歌唱与舞蹈两类节目，年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个．
1. （1）九年级师生表演的歌唱与舞蹈类节目数各有多少个？
2. （2）该校七、八年级师生有小品节目参与，在歌唱、舞蹈、小品三类节目中，每个节目的演出平均用时分别是5分钟、6分钟、8分钟，预计所有演出节目交接用时共花15分钟，若从20：00开始，22：30之前演出结束，问参与的小品类节目最多能有多少个？
答案解析收藏纠错 + 选题
13. (2017·青海)
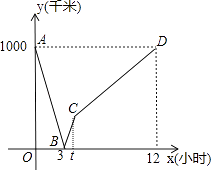
首条贯通丝绸之路经济带的高铁线﹣﹣宝兰客专进入全线拉通试验阶段，宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义，试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，两车同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示y与x之间的函数关系，根据图象进行一下探究：
1. （1）西宁到西安两地相距千米，两车出发后小时相遇；
2. （2）普通列车到达终点共需小时，普通列车的速度是千米/小时．
3. （3）求动车的速度；
4. （4）普通列车行驶t小时后，动车到达终点西宁，求此时普通列车还需行驶多少千米到达西安？
答案解析收藏纠错 + 选题
14. (2017·咸宁) 某公司开发出一款新的节能产品，该产品的成本价为6元/件，该产品在正式投放市场前通过代销点进行了为期一个月（30天）的试营销，售价为8元/件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象，图中的折线ODE表示日销售量y（件）与销售时间x（天）之间的函数关系，已知线段DE表示的函数关系中，时间每增加1天，日销售量减少5件．
1. （1）第24天的日销售量是件，日销售利润是元．
2. （2）求y与x之间的函数关系式，并写出x的取值范围；
3. （3）日销售利润不低于640元的天数共有多少天？试销售期间，日销售最大利润是多少元？
答案解析收藏纠错 + 选题

15. (2017·齐齐哈尔) 为养成学生课外阅读的习惯，各学校普遍开展了“我的梦中国梦”课外阅读活动，某校为了解七年级1200名学生课外日阅读所用时间情况，从中随机抽查了部分同学，进行了相关统计，整理并绘制出如下不完整的频数分布表和频数分布直方图，请根据图表信息解答下列问题：

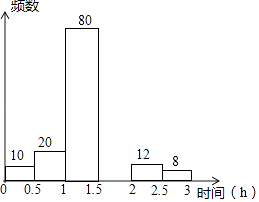
组别	时间段（小时）	频数	频率
1	0≤x＜0.5	10	0.05
2	0.5≤x＜1.0	20	0.10
3	1.0≤x＜1.5	80	b
4	1.5≤x＜2.0	a	0.35
5	2.0≤x＜2.5	12	0.06
6	2.5≤x＜3.0	8	0.04

（1）表中a=，b=；
（2）请补全频数分布直方图中空缺的部分；
（3）样本中，学生日阅读所用时间的中位数落在第组；
（4）请估计该校七年级学生日阅读量不足1小时的人数．

答案解析收藏纠错 + 选题

16. (2017·玉林) 在一个不透明的袋子中有一个黑球a和两个白球b，c（除颜色外其他均相同）．用树状图（或列表法）解答下列问题：
1. （1）小丽第一次从袋子中摸出一个球不放回，第二次又从袋子中摸出一个球．则小丽两次都摸到白球的概率是多少？
2. （2）小强第一次从袋子中摸出一个球，摸到黑球不放回，摸到白球放回；第二次又从袋子中摸出一个球，则小强两次都摸到白球的概率是多少？
答案解析收藏纠错 + 选题
17. (2021七下·沧县期末) 为加强中小学生安全教育，某校组织了“防溺水”知识竞赛，对表现优异的班级进行奖励，学校购买了若干副乒乓球拍和羽毛球拍，购买2副乒乓球拍和1副羽毛球拍共需116元；购买3副乒乓球拍和2副羽毛球拍共需204元．
1. （1）求购买1副乒乓球拍和1副羽毛球拍各需多少元；
2. （2）若学校购买乒乓球拍和羽毛球拍共30幅，且支出不超过1480元，则最多能够购买多少副羽毛球拍？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2018年中考数学专题高分攻略6讲专题五数学应用型问题

副标题：

*注意事项：

2018年中考数学专题高分攻略6讲专题五数学应用型问题

试题分析

总体分析

题量分析

难度分析

知识点分析