2015-2016学年浙江省金华十六中九年级上学期期末数学试...

更新时间：2017-01-05 浏览次数：937 类型：期末考试

一、仔细选一选

1. (2016九上·金华期末) 抛物线y=（x﹣2）²+3的对称轴是（）

A . 直线x=2 B . 直线x=3 C . 直线x=﹣2 D . 直线x=﹣3

答案解析收藏纠错 + 选题
2. (2016九上·金华期末) 两个相似多边形的面积之比是1：4，则这两个相似多边形的周长之比是（　　）

A . 1：2 B . 1：4 C . 1：8 D . 1：16

答案解析收藏纠错 + 选题
3. (2020九上·德清期末) 如图，⊙O的半径为5，弦心距OC=3，则弦AB的长是（）

A . 4 B . 6 C . 8 D . 5

答案解析收藏纠错 + 选题
4. (2016九上·金华期末) 如图，在△ABC中，DE∥BC，若 $\text{[math]}$ ，DE=4，则BC=（）

A . 9 B . 10 C . 11 D . 12

答案解析收藏纠错 + 选题
5. (2016九上·金华期末) 如图，直线l₁∥l₂∥l₃ ，直线AC分别交l₁ ， l₂ ， l₃于点A，B，C，直线DF分别交l₁ ， l₂ ， l₃于点D，E，F，已知AB=2，AC=5，DF=6，则DE的长是（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2016九上·金华期末) 分别把下列图形围起来得到的立体图形是圆锥的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2017·衡阳模拟) 如图，四边形ABCD内接于⊙O，已知∠ADC=130°，则∠AOC的大小是（）

A . 80° B . 100° C . 60° D . 40°

答案解析收藏纠错 + 选题
8. (2016九上·金华期末) 在同一坐标平面内，图象不可能由函数y=2x²+1的图象通过平移变换、轴对称变换得到的函数是（）

A . y=2（x+1）²﹣1 B . y=2x²+3 C . y=﹣2x²﹣1 D . y= $\text{[math]}$ x²﹣1

答案解析收藏纠错 + 选题
9. (2017·芜湖模拟) 有四张背面一模一样的卡片，卡片正面分别写着一个函数关系式，分别是y=2x，y=x²﹣3（x＞0），y= $\text{[math]}$ （x＞0），y=﹣ $\text{[math]}$ （x＜0），将卡片顺序打乱后，随意从中抽取一张，取出的卡片上的函数是y随x的增大而增大的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
10. (2016九上·金华期末) 如图，在平面直角坐标系中，A（﹣5，0），B（0，10），C（8，0），⊙A的半径为5．若F是⊙A上的一个动点，线段CF与y轴交于E点，则△CBE面积的最大值是（）

A . $\text{[math]}$ B . 40 C . 20 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、认真填一填

11. (2016九上·金华期末) 如图，某登山运动员从营地A沿坡度为1： $\text{[math]}$ 的斜坡AB到达山顶B，如果AB=1000米，则他实际上升了米．

答案解析收藏纠错 + 选题
12. (2016九上·金华期末) 如图，抛物线y₁=﹣x²+4x和直线y₂=2x在同一直角坐标系中．当y₁＞y₂时，x的取值范围是．

答案解析收藏纠错 + 选题
13. 如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3cm，则此光盘的直径是 cm．

答案解析收藏纠错 + 选题
14. (2016九上·金华期末) 已知 $\text{[math]}$ = $\text{[math]}$ ，那么 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
15. (2016九上·金华期末) 如图，一块铁片边缘是由抛物线和线段AB组成，测得AB=20cm，抛物线的顶点到AB边的距离为25cm．现要沿AB边向上依次截取宽度均为4cm的矩形铁皮，从下往上依次是第一块，第二块…如图所示．已知截得的铁皮中有一块是正方形，则这块正方形铁皮是第块．

答案解析收藏纠错 + 选题
16. (2016九上·金华期末) 如图，边长为2的正三角形ABC中，P₀是BC边的中点，一束光线自P₀发出射到AC上的点P₁后，依次反射到AB、BC上的点P₂和P₃（反射角等于入射角）．
1. （1）若∠P₂P₃B=45°，CP₁=；
2. （2）若 $\text{[math]}$ ＜BP₃＜ $\text{[math]}$ ，则P₁C长的取值范围是．
答案解析收藏纠错 + 选题

三、全面解一解

17. (2016九上·金华期末) 计算：（﹣ $\text{[math]}$ ）^﹣¹+ $\text{[math]}$ tan30°﹣sin²45°+（2016﹣cos60°）⁰ ．

答案解析收藏纠错 + 选题
18. (2016九上·金华期末) 一个直四棱柱的三视图如图所示，俯视图是一个菱形，求这个直四棱柱的表面积．

答案解析收藏纠错 + 选题
19. (2016九上·金华期末) 如图分别是某型号跑步机的实物图和示意图，已知踏板CD长为2米，支架AC长为0.8米，CD与地面的夹角为12°，∠ACD=80°，（AB‖ED），求手柄的一端A离地的高度h．（精确到0.1米，参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）

答案解析收藏纠错 + 选题
20. (2016九上·金华期末) 将两张半径均为10的半圆形的纸片完全重合叠放一起，上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形， $\text{[math]}$ 与直径AB交于点C，连接点C与圆心O′．
1. （1）求 $\text{[math]}$ 的长；
2. （2）求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S_白．
答案解析收藏纠错 + 选题
21. (2016九上·金华期末) 如图，⊙O是△ABC的外接圆，∠A=60°，过点C作⊙O的切线，交射线BO于点E．
1. （1）求∠BCE的度数；
2. （2）若⊙O半径为3，求BE长．
答案解析收藏纠错 + 选题
22. (2016九上·金华期末)
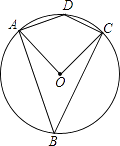
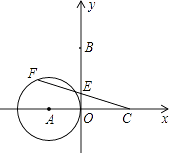
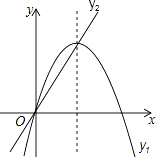
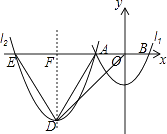
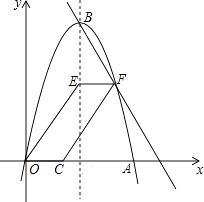
如图，抛物线y=﹣x²+6x与x轴交于点O，A，顶点为B，动点E在抛物线对称轴上，点F在对称轴右侧抛物线上，点C在x轴正半轴上，且EF $\text{[math]}$ OC，连接OE，CF得四边形OCFE．
1. （1）求B点坐标；
2. （2）当tan∠EOC= $\text{[math]}$ 时，显然满足条件的四边形有两个，求出相应的点F的坐标；
3. （3）当0＜tan∠EOC＜3时，对于每一个确定的tan∠EOC值，满足条件的四边形OCFE有两个，当这两个四边形的面积之比为1：2时，求tan∠EOC．
答案解析收藏纠错 + 选题
23. (2016九上·金华期末)
要利用28米长的篱笆和一堵最大可利用长为12米的墙围成一个如图1的一边靠墙的矩形养鸡场，在围建的过程中遇到了以下问题，请你帮忙来解决．
1. （1）这个矩形养鸡场要怎样建面积能最大？求出这个矩形的长与宽；
2. （2）在（1）的前提条件下，要在墙上选一个点P，用不可伸缩的绳子分别连接BP，CP，点P取在何处所用绳子长最短？
3. （3）仍然是矩形养鸡场面积最大的情况下，若把（2）中的不可伸缩的绳子改为可以伸缩且有弹性的绳子，点P可以在墙上自由滑动，求sin∠BPC的最大值．
答案解析收藏纠错 + 选题
24. (2016九上·金华期末)
如图，在平面直角坐标系中，抛物线l₁与x轴交于点A，B，与y轴交于点C，l₁的解析式为y= $\text{[math]}$ x²﹣2，若将抛物线l₁平移，使平移后的抛物线l₂经过点A，对称轴为直线x=﹣6，抛物线l₂与x轴的另一个交点是E，顶点是D，连结OD，AD，ED．
1. （1）求抛物线l₂的解析式；
2. （2）求证：△ADE∽△DOE；
3. （3）半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F（﹣6，0），运动速度为1单位/秒，运动时间为t秒，⊙P绕着点C顺时针旋转90°得⊙P₁ ，随着⊙P的运动，求P₁的运动路径长以及当⊙P₁与y轴相切的时候t的值．
答案解析收藏纠错 + 选题