2015-2016学年浙江省宁波市江北区九年级上学期期末数学...

更新时间：2017-01-04 浏览次数：862 类型：期末考试

一、选择题

1. (2016九上·江北期末) 若3x=2y，则x：y的值为（）

A . 2：3 B . 3：2 C . 3：5 D . 2：5

答案解析收藏纠错 + 选题
2. (2016九上·江北期末) 如果∠A是锐角，且sinA=cosA，那么∠A=（）

A . 30° B . 45° C . 60° D . 90°

答案解析收藏纠错 + 选题
3. (2016九上·江北期末) 圆锥的母线长为4，侧面积为12π，则底面半径为（）

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
4. (2016九上·江北期末) 一个袋子中有7只黑球，6只黄球，5只白球，一次性取出12只球，其中出现黑球是（）

A . 不可能事件 B . 必然事件 C . 随机事件 D . 以上说法均不对

答案解析收藏纠错 + 选题
5. (2016九上·江北期末) 下列函数中有最小值的是（）

A . y=2x﹣1 B . y=﹣ $\text{[math]}$ C . y=2x²+3x D . y=﹣x²+1

答案解析收藏纠错 + 选题
6. (2016九上·江北期末) 如果用表示1个立方体，用表示两个立方体叠加，用表示三个立方体叠加，那么下图由6个立方体叠成的几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2016九上·江北期末) ⊙O内有一点P，过点P的所有弦中，最长的为10，最短的为8，则OP的长为（）

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
8. (2016九上·江北期末) 下列m的取值中，能使抛物线y=x²+（2m﹣4）x+m﹣1顶点在第三象限的是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
9. (2016九上·江北期末) 四个直立在地面上的字母广告牌在不同情况下，在地面上的投影（阴影部分）效果如图．则在字母L，K，C的投影中，与字母N属同一种投影的有（）

A . L，K B . C C . K D . L，K，C

答案解析收藏纠错 + 选题
10. (2024九上·银州期末) 如图，圆内接四边形ABCD的BA，CD的延长线交于P，AC，BD交于E，则图中相似三角形有（）

A . 2对 B . 3对 C . 4对 D . 5对

答案解析收藏纠错 + 选题
11. (2016九上·江北期末) 如图，AB是⊙O的直径，弦CD⊥AB于点G．点F是CD上一点，且满足 $\text{[math]}$ = $\text{[math]}$ ，连接AF并延长交⊙0于点E．连接AD，DE，若CF=2，AF=3．给出下列结论：
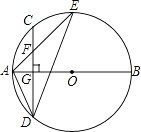
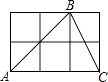
①△ADF∽△AED；②FG=2；③tan∠E= $\text{[math]}$ ；④S_△_DEF=4 $\text{[math]}$ ．
其中正确的是（）

A . ①②④ B . ①②③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
12. (2016九上·江北期末) 如图，在平面直角坐标系中，⊙P与y轴相切，交直线y=x于A，B两点，已知圆心P的坐标为（2，a）（a＞2），AB=2 $\text{[math]}$ ，则a的值为（）

A . 4 B . 2+ $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2016九上·江北期末) 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.1）．

答案解析收藏纠错 + 选题
14. (2018·绍兴模拟) 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么PB的长度为 cm．

答案解析收藏纠错 + 选题
15. (2016九上·江北期末) 如图，六个正方形组成一个矩形，A，B，C均在格点上，则∠ABC的正切值为．

答案解析收藏纠错 + 选题
16. (2016九上·江北期末) 如图，将一段12cm长的管道竖直置于地面，并在上面放置一个半径为5cm的小球，放置完毕以后小球顶端距离地面20cm，则该管道的直径AB为．

答案解析收藏纠错 + 选题
17. (2016九上·江北期末) 如图，将45°的∠AOB按下面的方式放置在一把刻度尺上：顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数恰为2cm．若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数约为 cm．（结果精确到0.1cm，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

答案解析收藏纠错 + 选题
18. (2016九上·江北期末) 如图，过y轴上一点P（0，1）作平行于x轴的直线PB，分别交函数y₁=x²（x≥0）与y₂= $\text{[math]}$ （x≥0）的图象于A₁ ， B₁两点，过点B₁作y轴的平行线交y₁的图象于点A₂ ，再过A₂作直线A₂B₂∥x轴，交y₂的图象于点B₂ ，依次进行下去，连接A₁A₂ ， B₁B₂ ， A₂A₃ ， B₂B₃ ， …，记△A₂A₁B₁的面积为S₁ ， △A₂B₁B₂的面积为S₂ ， △A₃A₂B₂的面积为S₃ ， △A₃B₂B₃的面积为S₄ ， …则S₂₀₁₆=

答案解析收藏纠错 + 选题

三、解答题

19. (2016九上·江北期末) 计算：2cos30°+| $\text{[math]}$ ﹣2|+（2016﹣π）⁰﹣（ $\text{[math]}$ ）^﹣¹ ．

答案解析收藏纠错 + 选题
20. (2016九上·江北期末) 如图，△ABC中，DE∥FG∥BC，AD：DF：FB=1：2：3，求S_四边形_DFGE：S_四边形_FBCG的值．

答案解析收藏纠错 + 选题
21. (2016九上·江北期末) 如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1m长的影子如图所示，已知窗框的影子DE到窗下墙脚的距离CE=3.9m，窗口底边离地面的距离BC=1.2m，试求窗口的高度．（即AB的值）

答案解析收藏纠错 + 选题
22. (2016九上·江北期末) 如图，PB切⊙O于点B，联结PO并延长交⊙O于点E，过点B作BA⊥PE交⊙O于点A，联结AP，AE．
1. （1）求证：PA是⊙O的切线；
2. （2）如果OD=3，tan∠AEP= $\text{[math]}$ ，求⊙O的半径．
答案解析收藏纠错 + 选题
23. (2016九上·崇仁期中) 甲、乙、丙三人之间相互传球，球从一个人手中随机传到另外一个人手中，共传球三次．
1. （1）若开始时球在甲手中，求经过三次传球后，球传回到甲手中的概率是多少？
2. （2）若乙想使球经过三次传递后，球落在自己手中的概率最大，乙会让球开始时在谁手中？请说明理由．
答案解析收藏纠错 + 选题
24. (2016九上·江北期末) 某商场销售一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量与销售单价基本满足一次函数关系，并且当销售单价为26元时，每天销售量28台；当销售单价为32元时，每天销售量16台，设台灯的销售单价为x（元），每天的销售量为y（台）．
1. （1）求y与x之间的函数关系式；
2. （2）当销售单价定为多少元时，每天的利润最大？最大利润是多少？
3. （3）若该商场每天想获得150元的利润，在保证销售量尽可能大的前提下，应将销售单价定为多少元？
答案解析收藏纠错 + 选题
25. (2016九上·江北期末)
由若干边长为1的小正方形拼成一系列“L”形图案（如图1）．
1. （1）当“L”形由7个正方形组成时，其周长为；
2. （2）如图2，过格点D作直线EF，分别交AB，AC于点E，F．
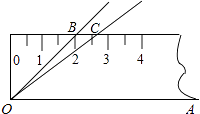
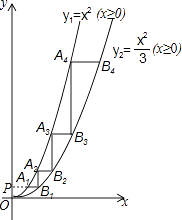
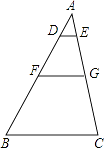
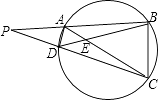
  ①试说明AE•AF=AE+AF；
  ②若“L”形由n个正方形组成时，EF将“L”形分割开，直线上方的面积为整个“L”形面积的一半，试求n的取值范围以及此时线段EF的长．
答案解析收藏纠错 + 选题
26. (2016九上·江北期末)
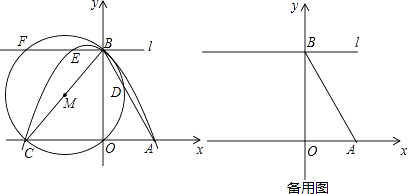
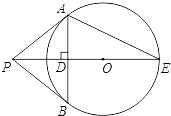
已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO= $\text{[math]}$ ，以线段BC为直径作⊙M交直线AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y=ax²+bx+c，直线l与抛物线和⊙M的另一个交点分别是E，F．
1. （1）求B点坐标；
2. （2）用含m的式子表示抛物线的对称轴；
3. （3）线段EF的长是否为定值？如果是，求出EF的长；如果不是，说明理由．
4. （4）是否存在点C（m，0），使得BD= $\text{[math]}$ AB？若存在，求出此时m的值；若不存在，说明理由．
答案解析收藏纠错 + 选题