2016-2017学年江苏省泰州市兴化市九年级上学期期中数学...

更新时间：2017-01-20 浏览次数：530 类型：期中考试

一、选择题

1. (2016九上·兴化期中) 在20人的青年歌手比赛中，规定前10 名晋级，某个选手想知道自己能否晋级，应该选取（）

A . 平均数 B . 众数 C . 中位数 D . 方差

答案解析收藏纠错 + 选题
2. (2016九上·兴化期中) 某中学人数相等的甲、乙两班学生参加了同一次数学测验，班平均分和方差分别为 $\text{[math]}$ _甲=82分， $\text{[math]}$ _乙=82分，S_甲²=245，S_乙²=190，那么成绩较为整齐的是（）

A . 甲班 B . 乙班 C . 两班一样整齐 D . 无法确定

答案解析收藏纠错 + 选题
3. (2021九上·韩城期末) 用扇形统计图反应地球上陆地面积与海洋面积所占比例时，陆地面积所对应的圆心角是108°，当宇宙中一块陨石落在地球上，则落在陆地上的概率是（）

A . 0.2 B . 0.3 C . 0.4 D . 0.5

答案解析收藏纠错 + 选题
4. (2016九上·兴化期中) 已知二次函数y=（x﹣2）²+3，当自变量x分别取3、5、7时，y对应的值分别为y₁、y₂、y₃ ，则y₁、y₂、y₃的大小关系正确的是（）

A . y₃＜y₁＜y₂ B . y₃＜y₂＜y₁ C . y₂＜y₁＜y₃ D . y₁＜y₂＜y₃

答案解析收藏纠错 + 选题
5. (2021九上·丹棱期中) 根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（　　）
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09

A . 3＜x＜3.23 B . 3.23＜x＜3.24 C . 3.24＜x＜3.25 D . 3.25＜x＜3.26

答案解析收藏纠错 + 选题
6. (2023九上·孝昌开学考) 若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx²+m的图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

7. (2016九上·兴化期中) 五个数1，2，4，5，﹣2的极差是

答案解析收藏纠错 + 选题
8. (2016九上·兴化期中) 抛掷一枚均匀的硬币2次，2次抛掷的结果都是正面朝上的概率为

答案解析收藏纠错 + 选题
9. (2016九上·兴化期中) 数据3，2，1，5，﹣1，1的众数和中位数之和是

答案解析收藏纠错 + 选题
10. (2016九上·兴化期中) 某工厂共有50名员工，他们的月工资方差s²=20，现在给每个员工的月工资增加300元，那么他们新工资的方差是．

答案解析收藏纠错 + 选题
11. (2016九上·兴化期中) 函数y=（m+2） $\text{[math]}$ +2x﹣1是二次函数，则m=．

答案解析收藏纠错 + 选题
12. (2021九上·松山期中) 某厂今年一月份新产品的研发资金为1000元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y（元）关于x的函数关系式为y=

答案解析收藏纠错 + 选题
13. 已知某种礼炮的升空高度h（m）与飞行时间t（s）的关系式是h=﹣ $\text{[math]}$ t²+20t+1．若此礼炮在升空到最高处时引爆，则引爆需要的时间为．

答案解析收藏纠错 + 选题
14. (2022九上·通海期中) 把抛物线y=x²﹣2x向下平移2个单位长度，再向右平移1个单位长度，则平移后的抛物线相应的函数表达式为．

答案解析收藏纠错 + 选题
15. (2016九上·兴化期中) 某学校九（1）班40名同学的期中测试成绩分别为a₁ ， a₂ ， a₃ ， …，a₄₀ ．已知a₁+a₂+a₃+…+a₄₀=4800，y=（a﹣a₁）²+（a﹣a₂）²+（a﹣a₃）²+…+（a﹣a₄₀）² ，当y取最小值时，a的值为

答案解析收藏纠错 + 选题
16. (2016九上·兴化期中) 若抛物线y=x²﹣4x+t（t为实数）在0≤x≤3的范围内与x轴有公共点，则t的取值范围为．

答案解析收藏纠错 + 选题

三、解答题

17. (2016九上·兴化期中) 综合题
1. （1）已知二次函数y=ax²+bx+1的图象经过点（1，3）和（3，﹣5），求a、b的值；
2. （2）已知二次函数y=﹣x²+bx+c的图象与x轴的两个交点的横坐标分别为1和2．求这个二次函数的表达式．
答案解析收藏纠错 + 选题
18. (2016九上·兴化期中) 甲、乙两位同学参加数学综合素质测试，各项成绩如下（单位：分）
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
1. （1）分别计算甲、乙成绩的中位数；
2. （2）如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3：3：2：2计算，那么甲、乙的数学综合素质成绩分别为多少分？
答案解析收藏纠错 + 选题
19. (2016九上·兴化期中) 某市今年中考理、化实验操作考试，采用学生抽签方式决定自己的考试内容．规定：每位考生必须在三个物理实验（用纸签A、B、C表示）和三个化学实验（用纸签D、E、F表示）中各抽取一个进行考试，小刚在看不到纸签的情况下，分别从中各随机抽取一个．
1. （1）用“列表法”或“树状图法”表示所有可能出现的结果；
2. （2）小刚抽到物理实验B和化学实验F（记作事件M）的概率是多少？
答案解析收藏纠错 + 选题
20. (2016九上·兴化期中) 市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
1. （1）根据表格中的数据，分别计算甲、乙的平均成绩；
2. （2）已知甲六次成绩的方差S_甲²= $\text{[math]}$ ，试计算乙六次测试成绩的方差；根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
答案解析收藏纠错 + 选题
21. (2018九上·青海期中) 在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同）．其中白球、黄球各1个，若从中任意摸出一个球是白球的概率是 $\text{[math]}$ ．
1. （1）求暗箱中红球的个数．
2. （2）先从暗箱中任意摸出一个球记下颜色后放回，再从暗箱中任意摸出一个球，求两次摸到的球颜色不同的概率（用树形图或列表法求解）．
答案解析收藏纠错 + 选题
22. (2017九上·温江期末) 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
1. （1）求y与x之间的函数关系式；
2. （2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
答案解析收藏纠错 + 选题
23. (2016九上·兴化期中) 国家规定，中小学生每天在校体育活动时间不低于1小时，为了解这项政策的落实情况，有关部门就“你某天在校体育活动时间是多少”的问题，在某校随机抽查了部分学生，再根据活动时间t（小时）进行分组（A组：t＜0.5，B组：0.5≤t＜1，C组：1≤t＜1.5，D组：t≥1.5），绘制成如下两幅不完整统计图，请根据图中信息回答问题：
1. （1）此次抽查的学生数为人，并补全条形统计图；
2. （2）从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是；
3. （3）若当天在校学生数为1200人，请估计在当天达到国家规定体育活动时间的学生有人．
答案解析收藏纠错 + 选题
24. (2016九上·兴化期中) 小明跳起投篮，球出手时离地面 $\text{[math]}$ m，球出手后在空中沿抛物线路径运动，并在距出手点水平距离4m处达到最高4m．已知篮筐中心距地面3m，与球出手时的水平距离为8m，建立如图所示的平面直角坐标系．
1. （1）求此抛物线对应的函数关系式；
2. （2）此次投篮，球能否直接命中篮筐中心？若能，请说明理由；若不能，在出手的角度和力度都不变的情况下，球出手时距离地面多少米可使球直接命中篮筐中心？
答案解析收藏纠错 + 选题
25. (2016九上·兴化期中) 已知二次函数y₁=x²﹣6x+9﹣t²和一次函数y₂=﹣2x﹣2t+6．
1. （1）当t=0时，试判断二次函数y₁的图象与x轴是否有公共点，如果有，请写出公共点的坐标；
2. （2）若二次函数y₁的图象与x轴的两个不同公共点，且这两个公共点间的距离为8，求t的值；
3. （3）求证：不论实数t取何值，总存在实数x，使y₁≥ty₂ ．
答案解析收藏纠错 + 选题
26. (2016九上·兴化期中) 在平面直角坐标系中，抛物线y=x²﹣6mx+5与y轴的交点为A，与x轴的正半轴分别交于点B（b，0），C（c，0）．
1. （1）当b=1时，求抛物线相应的函数表达式；
2. （2）
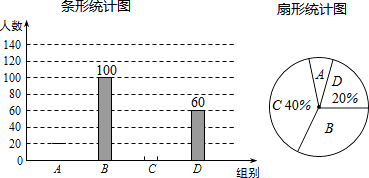
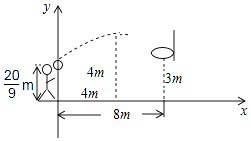
  当b=1时，如图，E（t，0）是线段BC上的一动点，过点E作平行于y轴的直线l与抛物线的交点为P．求△APC面积的最大值；
3. （3）当c=b+n时，且n为正整数，线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值．
答案解析收藏纠错 + 选题