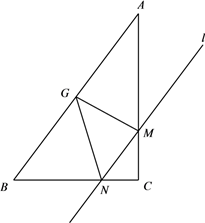江苏省无锡市滨湖区2018届数学调研考试试卷

更新时间：2018-07-31 浏览次数：464 类型：中考模拟

一、单选题

1. (2022·江苏模拟) 下列运算正确的是（）

A . (a³)²＝a⁶ B . 2a＋3a＝5a² C . a⁸÷a⁴＝a² D . a²·a³＝a⁶

答案解析收藏纠错 + 选题
2. (2018九下·滨湖模拟) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·安次模拟) 如图，一个由6个大小相同、棱长为1的正方体搭成的几何体，下列关于这个几何体的说法正确的是（）

A . 主视图的面积为6 B . 左视图的面积为2 C . 俯视图的面积为4 D . 俯视图的面积为3

答案解析收藏纠错 + 选题
4. (2021·斗门模拟) 如图，把等腰直角三角尺的直角顶点放在直尺的一边上，则∠1＋∠2的度数为（）

A . 60° B . 90° C . 120° D . 135°

答案解析收藏纠错 + 选题
5. (2018九下·滨湖模拟) 某校春季运动会比赛中，八年级（1）班、（2）班的竞技实力相当，关于比赛结果，甲同学说：（1）班与（2）班得分比为6：5；乙同学说：（1）班得分比（2）班得分的2倍少40分．若甲、乙两名同学的说法都正确，设（1）班得x分，（2）班得y分，根据题意所列的方程组应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·惠山模拟) 随着“互联网＋”时代的到来，一种新型的打车方式受到大众欢迎．打车总费用y（单位：元）与行驶里程x（单位：千米）的函数关系如图所示．如果小明某次打车行驶里程为22千米，则他的打车费用为（）

A . 33元 B . 36元 C . 40元 D . 42元

答案解析收藏纠错 + 选题
7. (2020·江阴模拟) 如图，在矩形纸片ABCD中，AB＝3，BC＝2，沿对角线AC剪开（如图①）；固定△ADC，把△ABC沿AD方向平移（如图②），当两个三角形重叠部分的面积最大时，移动的距离AA′等于（）

A . 1 B . 1.5 C . 2 D . 0.8或1.2

答案解析收藏纠错 + 选题
8. (2018九下·滨湖模拟) 如图，在平面直角坐标系中，A（0，2 $\text{[math]}$ ），动点B，C从原点O同时出发，分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动，以点A为圆心，OB的长为半径画圆；以BC为一边，在x轴上方作等边△BCD.设运动的时间为t秒，当⊙A与△BCD的边BD所在直线相切时，t的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 $\text{[math]}$ ＋6 D . 4 $\text{[math]}$ －6

答案解析收藏纠错 + 选题
9. (2019八上·乐亭期中) $\text{[math]}$ 等于（）

A . －4 B . 4 C . ±4 D . 256

答案解析收藏纠错 + 选题
10. (2021·张家界模拟) 下列说法中，正确的是（）

A . 为检测我市正在销售的酸奶质量，应该采用普查的方式 B . 若两名同学连续五次数学测试的平均分相同，则方差较大的同学数学成绩更稳定 C . 抛掷一个正方体骰子，朝上的面的点数为奇数的概率是 $\text{[math]}$ D . “打开电视，正在播放广告”是必然事件

答案解析收藏纠错 + 选题

二、填空题

11. (2018九下·滨湖模拟) 使 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
12. (2018九下·滨湖模拟) 分解因式：3x²－12＝．

答案解析收藏纠错 + 选题
13. (2020·江阴模拟) 2017年，无锡全市实现地区生产总值约10500亿元，成为继苏州、南京之后，江苏第三个GDP破万亿元的城市．将10500亿元这个数据用科学记数法表示为亿元．

答案解析收藏纠错 + 选题
14. (2020·江阴模拟) “微信发红包”是一种流行的娱乐方式，小红为了解家庭成员“除夕夜”使用微信发红包的情况，随机调查了15名亲戚朋友，结果如下表：
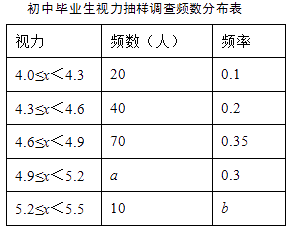
平均每个红包的钱数（元）
2
5
10
20
50
人数
7
4
2
1
1
则此次调查中平均每个红包的钱数的中位数为元．

答案解析收藏纠错 + 选题
15. (2020·江阴模拟) 一个圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是．

答案解析收藏纠错 + 选题
16. (2018九下·滨湖模拟) 如图，点G是△ABC的重心，AG的延长线交BC于点D，过点G作GE∥BC交AC于点E，如果BC＝6，那么线段GE的长为．

答案解析收藏纠错 + 选题
17. (2021·肇源模拟) 如图，正方形OABC的边长为8，A、C两点分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y＝ $\text{[math]}$ 的图像经过点Q，若S_△_BPQ＝ $\text{[math]}$ S_△_OQC ，则k的值为．

答案解析收藏纠错 + 选题
18. (2018九下·滨湖模拟) 如图，AB、CD是⊙O的两条互相垂直的直径，P为⊙O上一动点，过点P分别作PE⊥AB、PF⊥CD，垂足分别为E、F，M为EF的中点．若点P从点B出发，以每秒15°的速度按逆时针方向旋转一周，当∠MAB 取得最大值时，点P运动的时间为秒．

答案解析收藏纠错 + 选题

三、解答题

19. (2020·高邮模拟) 计算：
1. （1） 2tan45°－( $\text{[math]}$ －1)⁰＋ $\text{[math]}$ ；
2. （2） (a＋2b)²－(a＋b) (a－b)．
答案解析收藏纠错 + 选题
20. (2020·江阴模拟)
1. （1）解方程：x (x－2)＝3；
2. （2）解不等式组 $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2018九下·滨湖模拟) 如图，在△ABC中，∠ACB＝90°，CD为AB边上的中线，过点C作CE//AB，过点B作BE//CD，CE、BE相交于点E．求证：四边形BECD为菱形．

答案解析收藏纠错 + 选题
22. (2018九下·滨湖模拟) 某区对即将参加中考的4000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图．请根据图表信息回答下列问题：
1. （1）本次调查样本容量为；
2. （2）在频数分布表中，a＝，b＝，并将频数分布直方图补充完整；
3. （3）若视力在4.9以上（含4.9）均属标准视力，根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人？
答案解析收藏纠错 + 选题
23. (2020·江阴模拟) 2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类，每位考生只能在三类中各选一项进行考试．其中速度耐力类项目有：50米跑、800米跑、50米游泳；力量类项目有：掷实心球、引体向上；灵巧类项目有：30秒钟跳绳、立定跳远、俯卧撑、篮球运球．男生小明“50米跑”是强项，他决定必选，其它项目在平时测试中成绩完全相同，他决定随机选择．
1. （1）请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率；
2. （2）小明所选的项目中有立定跳远的概率是．
答案解析收藏纠错 + 选题
24. (2018九下·滨湖模拟) 如图，在由边长为1的小正方形组成的网格图中，有一个格点三角形ABC．（注：顶点均在网格线交点处的三角形称为格点三角形．）
1. （1） △ABC是三角形（填“锐角”、“直角”或“钝角”）；
2. （2）若P、Q分别为线段AB、BC上的动点，当PC＋PQ取得最小值时，
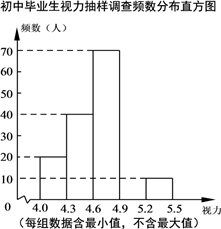
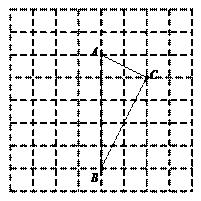
  ① 在网格中用无刻度的直尺，画出线段PC、PQ．（请保留作图痕迹．）
  ② 直接写出PC＋PQ的最小值：.
答案解析收藏纠错 + 选题
25. (2020·铁岭模拟) 如图，已知在⊙O中，AB是⊙O的直径，AC＝8，BC＝6．
1. （1）求⊙O的面积；
2. （2）若D为⊙O上一点，且△ABD为等腰三角形，求CD的长.
答案解析收藏纠错 + 选题
26. (2020·江阴模拟) 无锡水蜜桃享誉海内外，老王用3000元购进了一批水蜜桃.第一天，很快以比进价高40% 的价格卖出150千克．第二天，他发现剩余的水蜜桃卖相已不太好，于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出，本次生意老王一共获利750元．
1. （1）根据以上信息，请你编制一个问题，并给予解答；
2. （2）老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克，第二天，老王把卖相不好的水蜜桃挑出，单独打折销售，售价为10元/千克，结果很快被一抢而空，其余的仍按第一天的价格销售，且当天全部售完．若老王这次至少获利1100元，请问打折销售的水蜜桃最多多少千克？（精确到1千克．）
答案解析收藏纠错 + 选题
27. (2018九下·滨湖模拟) 如图，二次函数y＝ax²＋2ax－3a的图像与x轴交于A、B两点（点A在点B的右边），与y轴交于点C．
1. （1）请直接写出A、B两点的坐标：A， B；
2. （2）若以AB为直径的圆恰好经过这个二次函数图象的顶点．
  ①求这个二次函数的表达式；
  ②若P为二次函数图象位于第二象限部分上的一点，过点P作PQ平行于y轴，交直线BC于点Q．连接OQ、AQ，是否存在一个点P，使tan∠OQA＝ $\text{[math]}$ ？如果存在，请求出点P的坐标；如果不存在，请说明理由．
答案解析收藏纠错 + 选题
28. (2020·江阴模拟) 如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，G是边AB的中点，平行于AB的动直线l分别交△ABC的边CA、CB于点M、N，设CM＝m.
1. （1）当m＝1时，求△MNG的面积；
2. （2）若点G关于直线l的对称点为点G′，请求出点G′ 恰好落在△ABC的内部（不含边界）时，m的取值范围；
3. （3） △MNG是否可能为直角三角形？如果能，请求出所有符合条件的m的值；如果不能，请说明理由.
答案解析收藏纠错 + 选题