湖北省随州市2018年中考数学试卷

更新时间：2018-09-03 浏览次数：825 类型：中考真卷

一、选择题

1. (2023七上·洛川期末) ﹣ $\text{[math]}$ 的相反数是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . ﹣2 D . 2

答案解析收藏纠错 + 选题
2. (2020七上·岐山期末) 如图是一个由4个相同正方体组成的立体图形，它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2018·随州) 下列运算正确的是（）

A . a²•a³=a⁶ B . a³÷a^﹣³=1 C . （a﹣b）²=a²﹣ab+b² D . （﹣a²）³=﹣a⁶

答案解析收藏纠错 + 选题
4. (2020·鹤壁模拟) 如图，在平行线l₁、l₂之间放置一块直角三角板，三角板的锐角顶点A，B分别在直线l₁、l₂上，若∠l=65°，则∠2的度数是（）

A . 25° B . 35° C . 45° D . 65°

答案解析收藏纠错 + 选题
5. (2018·随州) 某同学连续6次考试的数学成绩分别是85，97，93，79，85，95，则这组数据的众数和中位数分别为（）

A . 85 和 89 B . 85 和 86 C . 89 和 85 D . 89 和 86

答案解析收藏纠错 + 选题
6. (2021九上·济阳期中) 如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则 $\text{[math]}$ 的值为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ -1 D . $\text{[math]}$ +1

答案解析收藏纠错 + 选题
7. (2024八下·巴州期中) “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先，但它因为骄傲在途中睡觉，而乌龟一直坚持爬行最终赢得比赛，下列函数图象可以体现这一故事过程的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2022·邯郸模拟) 正方形ABCD的边长为2，以各边为直径在正方形内画半圆，得到如图所示阴影部分，若随机向正方形ABCD内投一粒米，则米粒落在阴影部分的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020七上·林甸期末) 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1，3，6，10…）和“正方形数”（如1，4，9，16…），在小于200的数中，设最大的“三角形数”为m，最大的“正方形数”为n，则m+n的值为（）

A . 33 B . 301 C . 386 D . 571

答案解析收藏纠错 + 选题
10. (2022九上·莒南期中) 如图所示，已知二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x=1．直线y=﹣x+c与抛物线y=ax²+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：
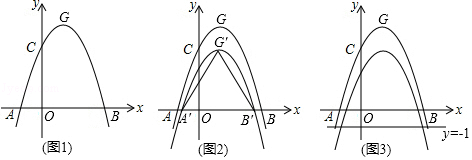
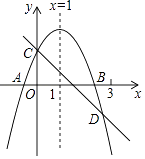
①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1．
其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

11. 计算： $\text{[math]}$ ﹣|2﹣2 $\text{[math]}$ |+2tan45°=．

答案解析收藏纠错 + 选题
12. (2018·随州) 如图，点A，B，C在⊙O上，∠A=40度，∠C=20度，则∠B=度．

答案解析收藏纠错 + 选题
13. (2024七下·南通期末) 已知 $\text{[math]}$ 是关于x，y的二元一次方程组 $\text{[math]}$ 的一组解，则a+b=．

答案解析收藏纠错 + 选题
14. (2018·随州) 如图，一次函数y=x﹣2的图象与反比例函数y= $\text{[math]}$ （k＞0）的图象相交于A、B两点，与x轴交与点C，若tan∠AOC= $\text{[math]}$ ，则k的值为．

答案解析收藏纠错 + 选题
15. (2018·随州) 如图，在平面直角坐标系xOy中，菱形OABC的边长为2，点A在第一象限，点C在x轴正半轴上，∠AOC=60°，若将菱形OABC绕点O顺时针旋转75°，得到四边形OA′B′C′，则点B的对应点B′的坐标为．

答案解析收藏纠错 + 选题
16. (2018·随州) 如图，在四边形ABCD中，AB=AD=5，BC=CD且BC＞AB，BD=8．给出以下判断：
①AC垂直平分BD；②四边形ABCD的面积S=AC•BD；③顺次连接四边形ABCD的四边中点得到的四边形可能是正方形；④当A，B，C，D四点在同一个圆上时，该圆的半径为 $\text{[math]}$ ；⑤将△ABD沿直线BD对折，点A落在点E处，连接BE并延长交CD于点F，当BF⊥CD时，点F到直线AB的距离为 $\text{[math]}$ ．其中正确的是．（写出所有正确判断的序号）

答案解析收藏纠错 + 选题

三、解答题

17. (2018·随州) 先化简，再求值： $\text{[math]}$ ，其中x为整数且满足不等式组 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2019九上·靖远月考) 已知关于x的一元二次方程x²+（2k+3）x+k²=0有两个不相等的实数根x₁ ， x₂ ．
1. （1）求k的取值范围；
2. （2）若 $\text{[math]}$ =﹣1，求k的值．
答案解析收藏纠错 + 选题
19. (2018·随州) 为了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘成如图所示的频数分布直方图，已知成绩x（单位：分）均满足“50≤x＜100”．根据图中信息回答下列问题：
1. （1）图中a的值为；
2. （2）若要绘制该样本的扇形统计图，则成绩x在“70≤x＜80”所对应扇形的圆心角度数为度；
3. （3）此次比赛共有300名学生参加，若将“x≥80”的成绩记为“优秀”，则获得“优秀“的学生大约有人：
4. （4）在这些抽查的样本中，小明的成绩为92分，若从成绩在“50≤x＜60”和“90≤x＜100”的学生中任选2人，请用列表或画树状图的方法，求小明被选中的概率．
答案解析收藏纠错 + 选题
20. (2018·随州) 随州市新㵐水一桥（如图1）设计灵感来源于市花﹣﹣兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔AB和斜拉索（图中只画出最短的斜拉索DE和最长的斜拉索AC）均在同一水平面内，BC在水平桥面上．已知∠ABC=∠DEB=45°，∠ACB=30°，BE=6米，AB=5BD．
1. （1）求最短的斜拉索DE的长；
2. （2）求最长的斜拉索AC的长．
答案解析收藏纠错 + 选题
21. (2020·中模拟) 如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．
1. （1）求证：MD=MC；
2. （2）若⊙O的半径为5，AC=4 $\text{[math]}$ ，求MC的长．
答案解析收藏纠错 + 选题
22. (2021·内江模拟) 为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第x天（1≤x≤15，且x为整数）每件产品的成本是p元，p与x之间符合一次函数关系，部分数据如表：
天数（x）
1
3
6
10
每件成本p（元）
7.5
8.5
10
12
任务完成后，统计发现工人李师傅第x天生产的产品件数y（件）与x（天）满足如下关系：y= $\text{[math]}$ ，
设李师傅第x天创造的产品利润为W元．
1. （1）直接写出p与x，W与x之间的函数关系式，并注明自变量x的取值范围：
2. （2）求李师傅第几天创造的利润最大？最大利润是多少元？
3. （3）任务完成后．统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？
答案解析收藏纠错 + 选题
23. (2018·随州) 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将 $\text{[math]}$ 化为分数形式
由于 $\text{[math]}$ =0.777…，设x=0.777…①
则10x=7.777…②
②﹣①得9x=7，解得x= $\text{[math]}$ ，于是得 $\text{[math]}$ = $\text{[math]}$ ．
同理可得 $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ =1+ $\text{[math]}$ =1+ $\text{[math]}$ ，
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
1. （1） $\text{[math]}$ =， $\text{[math]}$ =；
2. （2）将 $\text{[math]}$ 化为分数形式，写出推导过程；
3. （3） $\text{[math]}$ =， $\text{[math]}$ =；
  （注： $\text{[math]}$ =0.315315…， $\text{[math]}$ =2.01818…）
4. （4）（探索发现）
  ①试比较 $\text{[math]}$ 与1的大小： $\text{[math]}$ 1（填“＞”、“＜”或“=”）
  ②若已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ =．
  （注： $\text{[math]}$ =0.285714285714…）
答案解析收藏纠错 + 选题
24. (2018·随州) 如图1，抛物线C₁：y=ax²﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C₁的顶点为G．
1. （1）求出抛物线C₁的解析式，并写出点G的坐标；
2. （2）如图2，将抛物线C₁向下平移k（k＞0）个单位，得到抛物线C₂ ，设C₂与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：
3. （3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C₁、C₂于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．
答案解析收藏纠错 + 选题