 B .
B .  C .
C .  D .
D . 
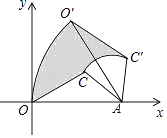
收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
按如下分数段整理、描述这两组样本数据:

在表中:m=,n=.
①两组样本数据的平均数、中位数、众数如表所示:
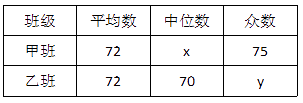
在表中:x=,y=.
②若规定测试成绩在80分(含80分)以上的叙述身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
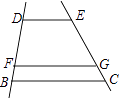
请根据图中信息解答下列问题:

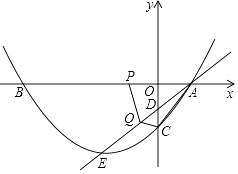
①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.
②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.