江苏省东台市第五联盟2018-2019学年八年级上学期数学第...

更新时间：2018-11-27 浏览次数：323 类型：月考试卷

一、单选题

1. (2020八上·兰山期中) 在下面的汽车标志图形中，是轴对称图形有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2020八上·淮滨期末) 到三角形三个顶点的距离都相等的点是这个三角形的（）

A . 三条高的交点 B . 三条角平分线的交点 C . 三条中线的交点 D . 三条边的垂直平分线的交点

答案解析收藏纠错 + 选题
3. (2018八上·东台月考) 小明不慎将一块三角形的玻璃摔碎成四块（即图中标有1、2、3、4的四块），如果将其中的哪一块带去玻璃店，就能配一块与原来一样大小的三角形玻璃．应该带（）

A . 第1块 B . 第2块 C . 第3块 D . 第4块

答案解析收藏纠错 + 选题
4. (2018八上·东台月考) 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C 画一条射线AE，AE就是∠PRQ的平分线。此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是（）

A . SSS B . SAS C . ASA D . AAS

答案解析收藏纠错 + 选题
5. (2018八上·东台月考) 如图，将一张长方形纸片沿对角线AC折叠后，点D落在点E处，与BC交于点F，图中全等三角形（包含△ADC）对数有（）

A . 1对 B . 2对 C . 3对 D . 4对

答案解析收藏纠错 + 选题
6. (2018八上·东台月考) ∠AOB的平分线上一点P到OA的距离为3，Q是OB上任一点，则（）

A . PQ＞3 B . PQ≥3 C . PQ＜3 D . PQ≤3

答案解析收藏纠错 + 选题
7. (2018八上·洛阳期中) 如图，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF的长是（）

A . 4cm B . 6cm C . 8cm D . 9cm

答案解析收藏纠错 + 选题
8. (2018八上·东台月考) 如图所示，已知△ABC和△BDE都是等边三角形．则下列结论：①AE=CD；②BF=BG；③∠AHC=60°；④△BFG是等边三角形；⑤HB平分∠AHD．其中正确的有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题

9. (2018八上·东台月考) 如图1，已知AB=AC，D为∠BAC的角平分线上面一点，连接BD，CD；如图2，已知AB=AC，D、E为∠BAC的角平分线上面两点，连接BD，CD，BE，CE；如图3，已知AB=AC，D、E、F为∠BAC的角平分线上面三点，连接BD，CD，BE，CE，BF，CF；…，依次规律，第n个图形中有全等三角形的对数是。

答案解析收藏纠错 + 选题
10. (2019八上·东台期中) 写出一个你熟悉的轴对称图形的名称：．

答案解析收藏纠错 + 选题
11. (2018八上·东台月考) 小明照镜子的时候，发现T恤上的英文单词在镜子中呈现“ ”的样子，请你判断这个英文单词是．

答案解析收藏纠错 + 选题
12. (2017八上·江门月考) 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是.

答案解析收藏纠错 + 选题
13. (2018八上·东台月考) 如图，在△ABC中，AB=AC，DE是AB的中垂线，△BCE的周长为16，BC=7，则AB的长为.

答案解析收藏纠错 + 选题
14. (2018八上·东台月考) 如图，在△ABC中，∠C=90°，AD平分∠BAC，BC=15，BD：CD=3：2，则点D到AB 的距离是．

答案解析收藏纠错 + 选题
15. (2018八上·东台月考) 如图所示，E，D是AB，AC上的两点，BD，CE交于点O，且AB=AC，使△ACE≌△ABD，你补充的条件是

答案解析收藏纠错 + 选题
16. (2018八上·东台月考) 如图，有一个直角△ABC，∠C=90°，AC=6，BC=3，一条线段PQ=AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问：当AP=时，才能使以点P、A、Q为顶点的三角形与△ABC全等．

答案解析收藏纠错 + 选题

三、解答题

17. (2018八上·东台月考) 已知：如图点A、B、C、D在一条直线上，EA∥FB，EC∥FD，AB=CD，求证：EA=FB．

答案解析收藏纠错 + 选题
18. (2018八上·东台月考) 已知：如图，∠B=∠D，∠1=∠2，AB=AD．求证：AC=AE．

答案解析收藏纠错 + 选题
19. (2018八上·东台月考) 在图示的方格纸中，
1. （1）画出△ABC关于MN对称的图形△A₁B₁C₁；
2. （2）说明△A₂B₂C₂是由△A₁B₁C₁经过怎样的平移得到的？
3. （3）在直线MN上找一点P，使得PB+PA最短．（不必说明理由）．
答案解析收藏纠错 + 选题
20. (2021八上·江都月考) 如图，已知：在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD．图中的CE、BD有怎样的大小和位置关系？试证明你的结论．

答案解析收藏纠错 + 选题
21. (2018八上·东台月考) 某国际帆船中心外形形状是一个三角形，要在它的内部修建一处公共服务设施（用点P表示），使它到三条路AB、BC、AC的距离相等．
1. （1）在图中确定公共服务设施P的位置．（不写作法，保留作图痕迹）
2. （2）若∠BAC=78°，试求∠BPC的度数．
答案解析收藏纠错 + 选题
22. (2018八上·东台月考) 如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．
1. （1）求证：BE=CF；
2. （2）如果AB=8，AC=6，求AE、BE的长．
答案解析收藏纠错 + 选题
23. (2018八上·东台月考) 已知∠AOB=90°，OC是∠AOB的平分线，按以下要求解答问题．
1. （1）将三角板的直角顶点P在射线OC上移动，两直角边分别与OA，OB交于M，N，如图①，求证：PM=PN；
2. （2）将三角板的直角顶点P在射线OC上移动，一条直角边与OB交于N，另一条直角边与射线OA的反向延长线交于点M，并猜想此时①中的结论PM=PN是否成立，并说明理由．
答案解析收藏纠错 + 选题
24. (2018八上·东台月考)
1. （1）【问题引领】
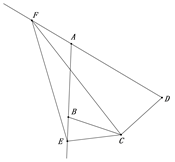
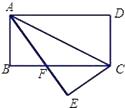
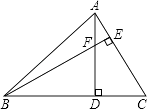
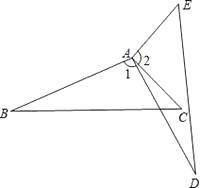
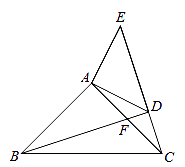
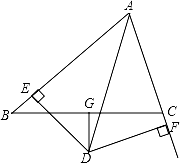
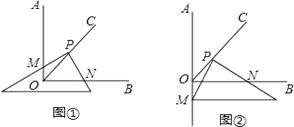
  问题1：在四边形ABCD中，CB=CD，∠B=∠ADC=90°，∠BCD=120°．E，F分别是AB，AD上的点．且∠ECF=60°．探究图中线段BE，EF，FD之间的数量关系．
  小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结CG，先证明△CBE≌△CDG，再证明△CEF≌△CGF．他得出的正确结论是．
2. （2）【探究思考】
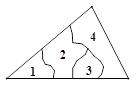
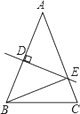
  问题2：若将问题1的条件改为：四边形ABCD中，CB=CD，∠ABC+∠ADC=180°，∠ECF= $\text{[math]}$ ∠BCD，问题1的结论是否仍然成立？请说明理由．
3. （3）【拓展延伸】
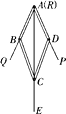
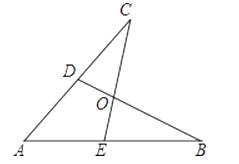
  问题3：在问题2的条件下，若点E在AB的延长线上，点F在DA的延长线上，则问题2的结论是否仍然成立？若不成立，猜测此时线段BE、DF、EF之间存在什么样的等量关系？并说明理由．
答案解析收藏纠错 + 选题