江苏省扬州市邵樊片2018-2019学年八年级上学期数学期中...

更新时间：2024-07-13 浏览次数：306 类型：期中考试

一、单选题

1. (2018八上·扬州期中) 下列都是同学们喜欢的商标，其中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2018八上·扬州期中) 在实数 $\text{[math]}$ 中，无理数有（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2018八上·扬州期中) 一等腰三角形的两边长分别为4和8，则这个等腰三角形的周长为（）

A . 16 B . 20 C . 18 D . 16或20

答案解析收藏纠错 + 选题
4. (2018八上·扬州期中) 下列是勾股数的是（）

A . 12，15，18 B . 6，10，7 C . D . 11，60，61

答案解析收藏纠错 + 选题
5. (2018八上·扬州期中) 如图，在△ABC中，BC=8，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长为18，则AC的长等于（）

A . 6 B . 8 C . 10 D . 12

答案解析收藏纠错 + 选题
6. (2018八上·扬州期中) 如图，在Rt△ABC中，∠ACB=90°，CD是高，AC=4，BC=3，则线段CD的长为（）

A . 5 B . C . D .

答案解析收藏纠错 + 选题
7. (2018八上·扬州期中)
在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（　　）

A . M点 B . N点 C . P点 D . Q点

答案解析收藏纠错 + 选题
8. (2018八上·扬州期中) 如图，图1是AD∥BC的一张纸条，按图1→图2→图3，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE=18°，则图2中∠AEF的度数为（）

A . 120° B . 108° C . 126° D . 114°

答案解析收藏纠错 + 选题

二、填空题

9. (2018八上·扬州期中) 已知△ABC≌△FED，∠A=20°，∠B=80°，则∠D=.

答案解析收藏纠错 + 选题
10. (2018八上·扬州期中) 某市今年参加中考的学生人数大约 $\text{[math]}$ 人，这个近似数精确到位.

答案解析收藏纠错 + 选题
11. (2018八上·扬州期中) 如图，∠ACB＝∠DFE，BC＝EF，可以补充一个直接条件，就能使△ABC≌△DEF.

答案解析收藏纠错 + 选题
12. (2018八上·扬州期中) 若一个正数的平方根分别是 $\text{[math]}$ 和 $\text{[math]}$ ，则这个数是

答案解析收藏纠错 + 选题
13. (2018八上·扬州期中) 一个等腰三角形的一个内角为50°，这个等腰三角形的一条腰上的高与底边的夹角是.

答案解析收藏纠错 + 选题
14. (2018八上·扬州期中) 如图所示，在△ABC中，∠C=90°，AD平分∠CAB，AC=8 cm，AD=10cm，那么D点到直线AB的距离是cm.

答案解析收藏纠错 + 选题
15. (2018八上·扬州期中) 如图所示，△ABC中，BA=5，BC=10，∠ABC的角平分线上有一点D，DE⊥AC于点E且AE=EC，DF⊥BC于点F，则CF=.

答案解析收藏纠错 + 选题
16. (2024八上·海曙期末) 如图，∠MON=90°，已知△ABC中，AC=BC=25，AB=14，△ABC的顶点A、B分别在边OM、ON上，当点B在边ON上运动时，A随之在OM上运动，△ABC的形状始终保持不变，在运动的过程中，点C到点O的最小距离为.

答案解析收藏纠错 + 选题

三、解答题

17. (2018八上·扬州期中)
1. （1）计算： $\text{[math]}$ ；
2. （2）求x的值： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2018八上·扬州期中) 已知 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，求x+4y的算术平方根.

答案解析收藏纠错 + 选题
19. (2018八上·扬州期中) 如图所示，在边长为1个单位长度的小正方形组成的网格中，给出了格点 $\text{[math]}$ 和 $\text{[math]}$ （顶点为网格线的交点），以及过格点的直线l.
1. （1） ①将 $\text{[math]}$ 向右平移3个单位长度，再向下平移1个单位长度，画出平移后的 $\text{[math]}$ .②画出 $\text{[math]}$ 关于直线l对称的 $\text{[math]}$
2. （2）填空：∠C+∠E=.
答案解析收藏纠错 + 选题
20. (2018八上·扬州期中) 如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE，过D作DG∥AC交BC于G.

求证：
1. （1） △GDF≌△CEF；
2. （2） △ABC是等腰三角形.
答案解析收藏纠错 + 选题
21. (2019八下·东莞月考) 如图，在5×5的方格纸中，每一个小正方形的边长都为1.
1. （1） ∠BCD是不是直角？请说明理由；
2. （2）求四边形ABCD的面积.
答案解析收藏纠错 + 选题
22. (2018八上·扬州期中) 如图，长方形的纸片ABCD中，AD=6cm，AB=8cm，把该纸片沿直线AC折叠，点B落在点E处，AE交DC于点F.
1. （1）图中有等腰三角形吗？为什么？
2. （2）求重叠部分（即△ACF）的面积.
答案解析收藏纠错 + 选题
23. (2020八上·吉州期末) 为了比较 $\text{[math]}$ +1与 $\text{[math]}$ 的大小，小伍和小陆两名同学对这个问题分别进行了研究.
1. （1）小伍同学利用计算器得到了 $\text{[math]}$ ， $\text{[math]}$ ，所以确定 $\text{[math]}$ +1 $\text{[math]}$ （填“＞”或“＜”或“=”）
2. （2）小陆同学受到前面学习在数轴上用点表示无理数的启发，构造出所示的图形，其中∠C=90°，BC=3，D在BC上且BD=AC=1.请你利用此图进行计算与推理，帮小陆同学对 $\text{[math]}$ +1和 $\text{[math]}$ 的大小做出准确的判断.
答案解析收藏纠错 + 选题
24. (2020八上·右玉期末) 如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，求证：M是BE的中点．

答案解析收藏纠错 + 选题
25. (2018八上·扬州期中) 如图
1. （1）发现：如图1，点A为一动点，点B和点C 为两个定点，且BC=a，AB=b.（a>b）
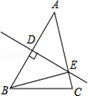
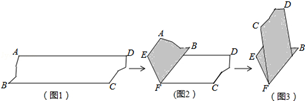
  填空：当点A位于时，线段AC的长取得最小值，且最小值为(用含a，b的式子表示)
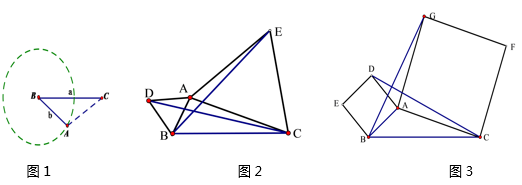
2. （2）应用：点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE.
  ①请找出图中与BE相等的线段，并说明理由；
  
  ②直接写出线段BE长的最小值.
  
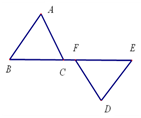
  ③如图3所示，分别以AB，AC为边，作正方形ADEB和正方形ACFG，连接CD，BG.写出图中线段CD，BG的关系，求线段BG的最大值
答案解析收藏纠错 + 选题
26. (2018八上·扬州期中) 如图A村和B村在一条大河CD的同侧，它们到河岸的距离AC、BD分别为1千米和4千米，又知道CD的长为4千米.
1. （1）现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
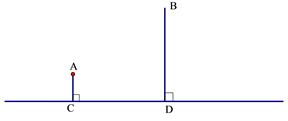
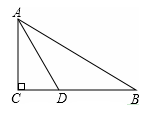
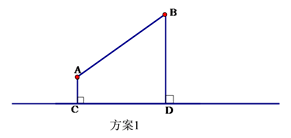
  方案1：水厂建在C点，修自来水管道到A村，再到B 村（即AC+AB）.（如图）
  
  方案2：作A点关于直线CD的对称点 $\text{[math]}$ ，连接 $\text{[math]}$ 交CD于M点，水厂建在M点处，分别向两村修管道AM和BM.（即AM+BM）（如图）
  
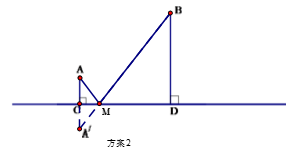
  从节约建设资金方面考虑，将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算，判断哪种方案更合适.
2. （2）有一艘快艇Q从这条河中驶过，当快艇Q与CD中点G相距多远时，△ABQ为等腰三角形？直接写出答案，不要说明理由.
答案解析收藏纠错 + 选题