江苏省东台市第七联盟2018-2019学年八年级上学期数学期...

更新时间：2019-06-26 浏览次数：385 类型：期中考试

一、单选题

1. (2018八上·东台期中) 下列汽车标志中是轴对称图形的有（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
2. (2018八上·东台期中) 下列实数中， $\text{[math]}$ （相邻两个3之间依次增加一个2），无理数的个数是（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
3. (2021八上·黄埔期末) 如图，给出下列四组条件：
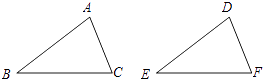
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E．BC=EF；
③∠B=∠E，BC=EF，∠C=∠F；
④AB=DE，AC=DF，∠B=∠E．
其中，能使△ABC≌△DEF的条件共有（）

A . 1组 B . 2组 C . 3组 D . 4组

答案解析收藏纠错 + 选题
4. (2018八上·东台期中) 下列四组数中不是勾股数的一组是（）

A . 4，5，6 B . 7，24，25 C . 5，12，13 D . 11，60，61

答案解析收藏纠错 + 选题
5. (2018八上·东台期中) 对于四舍五入得到的近似数 $\text{[math]}$ ，下列说法正确的是（）

A . 精确到百位 B . 精确到个位 C . 精确到万位 D . 精确到百分位

答案解析收藏纠错 + 选题
6. (2018八上·东台期中) 如图，AB⊥AC，AD⊥BC，垂足为D，AB=3，AC=4，AD= $\text{[math]}$ ，BD= $\text{[math]}$ ，则点B到直线AD的距离为（）

A . B . $\text{[math]}$ C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2018八上·东台期中) 在等腰三角形ABC中，AB=AC=8cm，腰AB的垂直平分线交另一腰AC于D，若△BCD的周长为10cm，则底边BC的长为（）

A . 1cm B . 2cm C . 3cm D . 4 cm

答案解析收藏纠错 + 选题
8. (2018八上·东台期中) 如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（）

A . B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题

二、填空题

9. (2018八上·东台期中) 若等腰三角形的一个角为70゜，则其顶角的度数为．

答案解析收藏纠错 + 选题
10. (2024八下·岷县月考) 若实数a、b满足|a+2|+ $\text{[math]}$ =0，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
11. (2018八上·东台期中) 已知一个直角三角形的两边长分别为5cm和12cm，则第三边为．

答案解析收藏纠错 + 选题
12. (2018八上·东台期中) 如图，已知Rt△ABC中，∠ACB=90°，D是AB的中点， CD=5cm，则AB=cm．

答案解析收藏纠错 + 选题
13. (2018八上·东台期中) 如图，是4×4正方形网格，其中已有4个小方格涂成了黑色．现在要从其余白色小方格中选出一个也涂成黑色，使整个黑色部分图形构成轴对称图形，这样的白色小方格有种选择.

答案解析收藏纠错 + 选题
14. (2018八上·东台期中) 如图，等边△ABC的两条中线BD、CE交于点O，则∠BOC= °．

答案解析收藏纠错 + 选题
15. (2018八上·东台期中) 已知正数的两个不同的平方根是和，则＝．

答案解析收藏纠错 + 选题
16. (2018八上·东台期中) 如图，OP=1，过P作PP₁⊥OP，得OP₁= $\text{[math]}$ ；再过P₁作P₁P₂⊥OP₁且P₁P₂=1，得OP₂= $\text{[math]}$ ；又过P₂作P₂P₃⊥OP₂且P₂P₃=1，得OP₃=2；……依此法继续作下去，得OP₂₀₁₆=．

答案解析收藏纠错 + 选题
17. (2021七上·芝罘期末) 如图，在锐角△ABC中，∠BAC=45°，AB=2，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是．

答案解析收藏纠错 + 选题

三、解答题

18. (2018八上·东台期中)
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$ ；
答案解析收藏纠错 + 选题
19. (2018八上·东台期中) 如图所示，要在公园（四边形ABCD）中建造一座音乐喷泉，喷泉位置应符合如下要求：

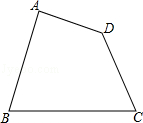
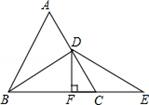
（ 1 ）到公园两个出入口A、C的距离相等；

（ 2 ）到公园两边围墙AB、AD的距离相等；

请你用尺规作图的方法确定喷泉的位置P．（不必写作法，但要保留作图痕迹）

答案解析收藏纠错 + 选题
20. 如图，AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F.求证：DE＝DF.

答案解析收藏纠错 + 选题
21. 如图，在△ABC中，AB=20，AC=15，BC=25，AD⊥BC，垂足为D．求AD，BD的长．

答案解析收藏纠错 + 选题
22. (2021八上·交口期末) 如图，等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DF⊥BE，垂足是F，求证：BF=EF．

答案解析收藏纠错 + 选题
23. (2018八上·东台期中) 已知2b+3的平方根是 $\text{[math]}$ ,3a+2b+1的算术平方根为4，
求：
1. （1） 3a+6b的立方根；
2. （2）已知a=5, $\text{[math]}$ ,求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
24. (2018八上·东台期中) 如图，将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE，连接BE，延长DE、BC相交于点F，则有∠BFE=90°，且四边形ACFD是一个正方形．
1. （1）判断△ABE的形状，并证明你的结论；
2. （2）用含b代数式表示四边形ABFE的面积；
3. （3）求证：a²+b²=c² ．
答案解析收藏纠错 + 选题
25. (2018八上·东台期中) 阅读下面材料，并解决问题：
1. （1）如图（1），等边△ABC内有一点P若点P到顶点A，B，C的距离分别为3，4，5欲求∠APB的度数，由于PA，PB不在一个三角形中，为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP这样，就可以利用全等三角形知识，将三条线段的长度转化到一个三角形中从而求出∠APB的度数．
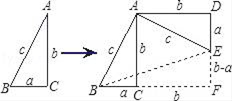
  请将下列解题过程补充完整。
  
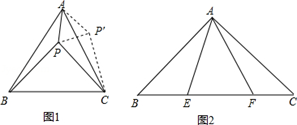
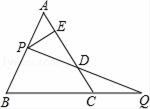
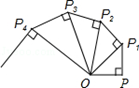
  ∵△ACP′≌△ABP，
  
  ∴AP′==3，CP′==4，∠=∠APB．
  
  由题意知旋转角∠PA P′=60°，∴△AP P′为三角形，
  
  P P′=AP=3，∠A P′P=60°。
  
  易证△P P′C为直角三角形，且∠P P′C=90°，
  
  ∴∠APB=∠AP′C=∠A P′P+∠P P′C=°+°=°.
2. （2）请你利用第（1）题的解答思想方法，解答下面问题：
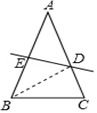
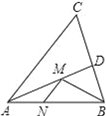
  已知如图（2），△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，
  
  求证：EF²=BE²+FC² ．
答案解析收藏纠错 + 选题