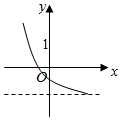
 B .
B . 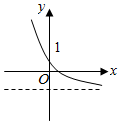 C .
C . 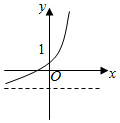 D .
D . 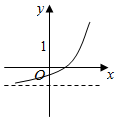
①当 时,函数
在
上是单调增函数;②当
时,函数
在
上有最小值;③函数
的图象关于点
对称;④方程
可能有三个实数根.
①c = 0时, 是奇函数; ②
时,方程
只有一个实根; ③
的图象关于点(0 , c)对称; ④方程
至多3个实根.
其中正确的命题个数是( )
| x | 1 | 2 | 3 | 4 |
| | | | | |
若 近似符合以下三种函数模型之一:
.