江苏省苏州市工业园区2016-2017学年八年级下学期期中考...

更新时间：2017-04-25 浏览次数：734 类型：期中考试

一、选择题：

1. (2017八下·苏州期中) 下列各式： $\text{[math]}$ ，其中分式共有（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
2. (2023八下·邗江期末) 下列式子中，y是 $\text{[math]}$ 的反比例函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2017八下·苏州期中) 分式 $\text{[math]}$ 有意义，则x的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2017八下·东台开学考) 在反比例函数y= $\text{[math]}$ 的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是（）．

A . k>1 B . k>0 C . k≥1 D . k<1

答案解析收藏纠错 + 选题
5. 如果把分式 $\text{[math]}$ 中的 $\text{[math]}$ 和 $\text{[math]}$ 都扩大3倍，那么分式的值（）

A . 不变 B . 扩大3倍 C . 缩小3倍 D . 扩大9倍

答案解析收藏纠错 + 选题
6. (2017八下·苏州期中)
如图，矩形ABCD对角线相交于点O ， ∠AOB＝60°，AB＝4，则AC的为（）

A . 4 B . 8 C . 4 $\text{[math]}$ D . 10

答案解析收藏纠错 + 选题
7. (2017八下·苏州期中)
如图，菱形ABCD中，∠BAD＝120°．若△ABC的周长是15，则菱形ABCD的周长是（）

A . 25 B . 20 C . 15 D . 10

答案解析收藏纠错 + 选题
8. (2017八下·苏州期中)
如图，在平行四边形ABCD中，BD为对角线，点E、O、F分别是 AB、BD、BC的中点，且OE＝3，OF＝2，则平行四边形ABCD的周长为（）

A . 10 B . 12 C . 15 D . 20

答案解析收藏纠错 + 选题
9. (2017·开封模拟) 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= $\text{[math]}$ 在第一象限的图象经过点B，则△OAC与△BAD的面积之差S_△_OAC﹣S_△_BAD为（）

A . 36 B . 12 C . 6 D . 3

答案解析收藏纠错 + 选题
10. (2017八下·苏州期中)
如图，在正方形OABC中，点B的坐标是（4，4），点E、F分别在边BC、BA上，OE=2 $\text{[math]}$ ，若∠EOF＝45°，则F点的纵坐标是（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$ -1

答案解析收藏纠错 + 选题

二、填空题。

11. (2017八下·苏州期中) 当x时，分式 $\text{[math]}$ 的值为0

答案解析收藏纠错 + 选题
12. (2017八下·苏州期中) ▱ABCD中，∠A+∠C=100°，则∠B=．

答案解析收藏纠错 + 选题
13. (2017八下·苏州期中) 若点(－1，2)在双曲线 $\text{[math]}$ 上，则此双曲线的函数表达式为．

答案解析收藏纠错 + 选题
14. (2022八上·盘山期末) 约分：① $\text{[math]}$ ，② $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2017八下·苏州期中) 若分式方程 $\text{[math]}$ =5＋ $\text{[math]}$ 有增根，则a的值为．

答案解析收藏纠错 + 选题
16. (2017八下·苏州期中)
如图，双曲线 $\text{[math]}$ $\text{[math]}$ 上有一点A，过点A作AB⊥x轴于点B，△AOB的面积为2，则该双曲线的表达式为 .

答案解析收藏纠错 + 选题
17. (2017八下·苏州期中)
正方形A₁B₁C₁O ， A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图的方式放置．点A₁ ， A₂ ， A₃ ， …和点
C₁ ， C₂ ， C₃ ， …分别在直线y=x+1和x轴上，则点B_n的坐标是 .

答案解析收藏纠错 + 选题
18. (2017八下·苏州期中)
如图，在坐标系中放置一菱形OABC ，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2015次，点B的落点依次为B₁ ， B₂ ， B₃ ， …，则B₂₀₁₅的坐标为．

答案解析收藏纠错 + 选题

三、解答题.

19. (2017八下·苏州期中) 计算：
1. （1） $\text{[math]}$ － $\text{[math]}$
2. （2） $\text{[math]}$ · $\text{[math]}$ ＋(3x+1)
答案解析收藏纠错 + 选题
20. (2017八下·苏州期中) 解方程：
1. （1） $\text{[math]}$
  ＋ $\text{[math]}$ =1
2. （2） $\text{[math]}$
  ＋ $\text{[math]}$ ＝ $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2017八下·苏州期中) 先化简，再求值：[1＋ $\text{[math]}$ ]÷ $\text{[math]}$ ，其中x＝6．

答案解析收藏纠错 + 选题
22. (2020八下·扬州期中)
如图，在△ABC中，AB＝AC ， D为边BC上一点，以AB、BD为邻边作平行四边形ABDE ，连接AD、EC ．若BD＝CD ，求证：四边形ADCE是矩形．

答案解析收藏纠错 + 选题
23. (2024九上·长岭期末)
如图是函数 $\text{[math]}$ 与函数 $\text{[math]}$ 在第一象限内的图象，点P是 $\text{[math]}$ 的图象上一动点，PA⊥x轴于点A ，交 $\text{[math]}$ 的图象于点C， PB⊥y轴于点B ，交 $\text{[math]}$ 的图象于点D．
1. （1）求证：D是BP的中点；
2. （2）求出四边形ODPC的面积．
答案解析收藏纠错 + 选题
24. (2017八下·苏州期中) 某车队要把4000吨货物运到雅安地震灾区（方案定后，每天的运量不变）。
1. （1）从运输开始，每天运输的货物吨数n（单位：吨）与运输时间t（单位：天）之间有怎样的函数关系式？
2. （2）因地震，到灾区的道路受阻，实际每天比原计划少运20%，则推迟1天完成任务，求原计划完成任务的天数．
答案解析收藏纠错 + 选题
25. (2017八下·苏州期中)
请按要求，只用无刻度的直尺作图（请保留画图痕迹，不写作法）
如图，已知∠AOB ， OA＝OB ，点E在OB边上，四边形AEBF是平行四边形，在图中画
出∠AOB的平分线．

答案解析收藏纠错 + 选题
26. (2017八下·苏州期中)
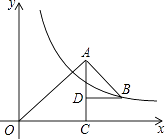
如图，在平面直角坐标系中，正比例函数y=kx（k>0）与反比例函数y= $\text{[math]}$ 的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为（m ， 0）．其中m>0．
1. （1）四边形ABCD的是．(填写四边形ABCD的形状)
2. （2）当点A的坐标为（n ， 3）时，四边形ABCD是矩形，求mn的值．
3. （3）试探究：随着k与m的变化，四边形ABCD能不能成为菱形？若能，请直接写出k的值；若不能，请说明理由．
答案解析收藏纠错 + 选题
27. (2017八下·苏州期中)
如图，在Rt△ABC中，∠BAC＝90°，AB＞AC ，射线AM平分∠BAC ．
1. （1）设AM交BC于点D ，作DE⊥AB于点E ， DF⊥AC于点F ，连接EF ．有以下三种“判断”：
  判断1：AD垂直平分EF．
  判断2：EF垂直平分AD．
  判断3：AD与EF互相垂直平分．
  你同意哪个“判断”？简述理由；
2. （2）若射线AM上有一点N到△ABC的顶点B ， C的距离相等，连接NB ， NC ．
  ①请指出△NBC的形状，并说明理由；
  ②当AB＝11，AC＝7时，求四边形ABNC的面积．
答案解析收藏纠错 + 选题